F = M a Olympiad Problem 1
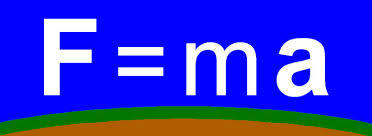 An observer stands on the side of the front of a stationary train. When the train starts moving with constant acceleration, it takes
5
seconds for the first car to pass the observer. How long, in seconds, will it take for the
1
0
th
car to pass?
An observer stands on the side of the front of a stationary train. When the train starts moving with constant acceleration, it takes
5
seconds for the first car to pass the observer. How long, in seconds, will it take for the
1
0
th
car to pass?
The answer is 0.81.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Let the length of each car be = s
For the first car, u = 0 and t = 5
Let acceleration be equal to a
Thus, s = u t + 2 1 a t 2 ⇒ s = ( 0 × 5 ) + 2 1 a ( 5 2 ) ⇒ s = 2 2 5 a ⇒ 2 5 2 s = a
The velocity v acquired after the passing of the 9 t h car would be given by v 2 = u 2 + 2 a s ⇒ v 2 = 0 + 2 ( 2 5 2 s ) ( 9 s ) ⇒ v 2 = 2 5 4 s × 9 s ⇒ v 2 = 2 5 3 6 s 2 ⇒ v = 5 6 s
Now, for the time taken by the 1 0 t h car to pass, we use the equation
s = u t + 2 1 a t 2
Applying the values, we get
s = 5 6 s t + 2 1 2 5 2 s t 2 ⇒ s = 5 6 s t + 2 5 s t 2 ⇒ s = 2 5 3 0 s t + s t 2 ⇒ 1 = 2 5 3 0 t + t 2 ⇒ 2 5 = 3 0 t + t 2
On solving the equation, we get
t = 5 ( − 3 − 1 0 ) t = 5 ( 1 0 − 3 )
Since time cannot be negative, we only have the second value of t
Thus t = 5 ( 1 0 − 3 ) = 5 ( 3 . 1 6 − 3 ) = 5 × . 1 6 = . 8 0
I found that it was easier to denote the length of each car simply as 1 because we are dealing with ratios in the question. Nice solution though :)
Awesome solution man!!
The distance is proportional to the square of the time. So, if the length of one train takes 5 seconds, 9 trains will take 5 sqrt(9) and 10 will take 5 sqrt(10). Therefore the tenth train will take 5*sqrt(10) - 15 = 0.81
Let the length of a train car be l . We know that the displacement s of the train travelling with constant acceleration a passes the observer after time t is given by:
s = u t + 2 1 a t 2 ⇒ s = 2 1 a t 2
where u = 0 is the initial velocity of the train.
Since it takes 5 s for the first car to pass by, we have:
l = 2 1 a ( 5 2 ) ⇒ a = 2 5 2 l
From s = 2 1 a t 2 = 2 5 l t 2 ⇒ t ( s ) = 5 l s .
So the time for the 1 0 t h to pass is given by:
t ( 1 0 l ) − t ( 9 l ) = 5 l 1 0 l − 5 l 9 l = 5 ( 1 0 − 3 ) ≈ 0 . 8 1 s.