Euclidean geometry is great!

Geometry Level 5

Using a straightedge and a compass, and given a line $\lambda$ and a point $A$ on the line, what is the minimum number of moves required to construct a line which makes a $30 ^ \circ$ angle with line $\lambda$ which passes through point $A$ ?

All terminology in this question is explained in Wen Z's note . Credits to Wen Z for making the note..

2 3 1 Not possible 5 6 -1 4

2 solutions

Manuel Kahayon
Oct 12, 2016

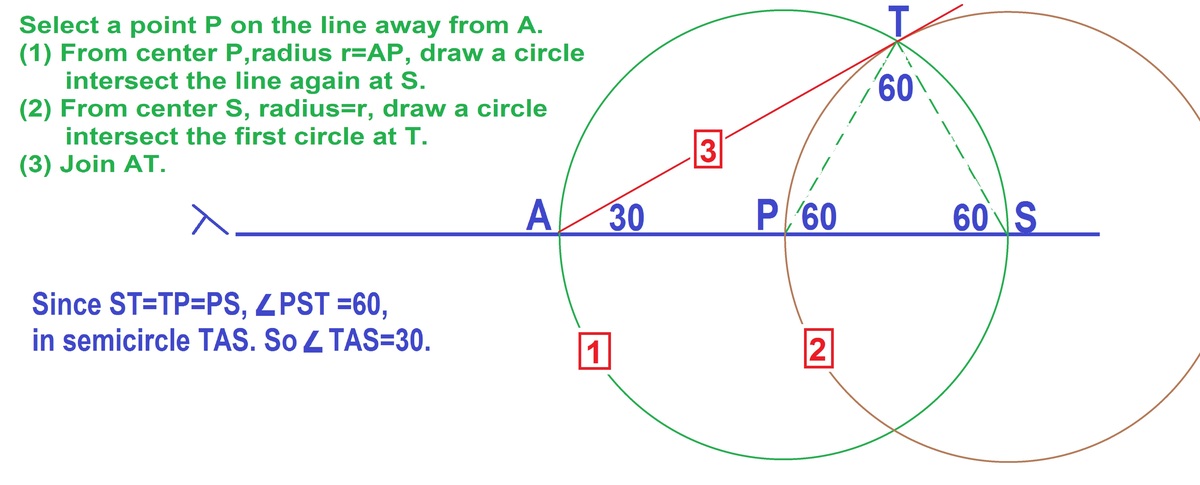
One can obviously not do it in 2 moves, as one move is to be used for creating the line, which leaves one last move for finding a point through which the line passes through, which is impossible since a minimum of 2 moves must be made to find a point on the line. We will then prove that it is possible in 3 moves.

Choose an arbitrary point $O$ on $\lambda$ not equal to $A$ . Draw a circle centered at $O$ , passing through $A$ and intersecting $\lambda$ at $K$ . Draw a circle centered at $K$ passing through $O$ . Now, let the two circles intersect at $B$ and $C$ . Now, since $\angle BOK = 60^\circ$ , and it is a central angle of the first circle, and $\angle BAK$ is an inscribed angle, therefore $\angle BAK = 30^\circ$ . We have used two moves so far, and drawing line $AB$ takes us $\boxed{3}$ moves.

Niranjan Khanderia
Oct 15, 2016

Woah! This is nice! What motivates you to consider this geometric construction?

Pi Han Goh - 4 years, 8 months ago

Thank you. I knew that the side of a regular hexagon equals to the circumradius, and the hexagon is made up of six equilateral triangles.

Niranjan Khanderia - 4 years, 7 months ago

Euclidean geometry is great!

2 solutions

0 pending reports