Which Part Should I Integrate?
Suppose that f is a smooth function (meaning that all orders of derivatives exist and are continuous) such that f ( 0 ) = 1 , f ( 2 ) = 3 and f ′ ( 2 ) = 5 , then evaluate
∫ 0 1 x f ′ ′ ( 2 x ) d x .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Watch out for when you can apply Integration by parts. It is a necessary condition that the functions u and v are continuously differentiable.
I forgot f(0) was 1, so got 5/2 -3/4 instead, so close
Relevant wiki: Integration by Parts - Intermediate
Substitute 2 x = t such that :- 4 I = ∫ 0 2 t f ′ ′ ( t ) d t
Now apply integration by parts:-
4 I = [ t f ′ ( t ) ] 0 2 − ∫ 0 2 f ′ ( t ) d t [ f ( t ) ] 0 2
= 2 f ′ ( 2 ) − ( f ( 2 ) − f ( 1 ) ) = 8
⟹ I = 2
NOTE:-
∵ d t d ( f ( t ) + C ) = f ′ ( t ) ∴ ∫ f ′ ( t ) d t = f ( t ) + C ∵ d t d ( f ′ ( t ) + C ) = f ′ ′ ( t ) ∴ ∫ f ′ ′ ( t ) d t = f ′ ( t ) + C C − Arbitrary real constant
Integrating by parts, let u = x, dv = f""(2x)dx. Then du = dx, v = (1/2)f"(2x).. (1/2)xf"(2x) - (1/2)*integral of f"(2x)dx , all evaluated from o to 1 gives: (1/2)f"2) - (1/4)f(2) + (1/4)f(0) = 5/2 - 3/4 + 1/4 = 2. Ed Gray
do integration by part!
let:
u = x and d v = f ′ ′ ( 2 x )
do it once again with
u = 1 and d v = 1 / 2 f ′ ( 2 x )
if you don't want to do some tedious work, do it in tabular way!
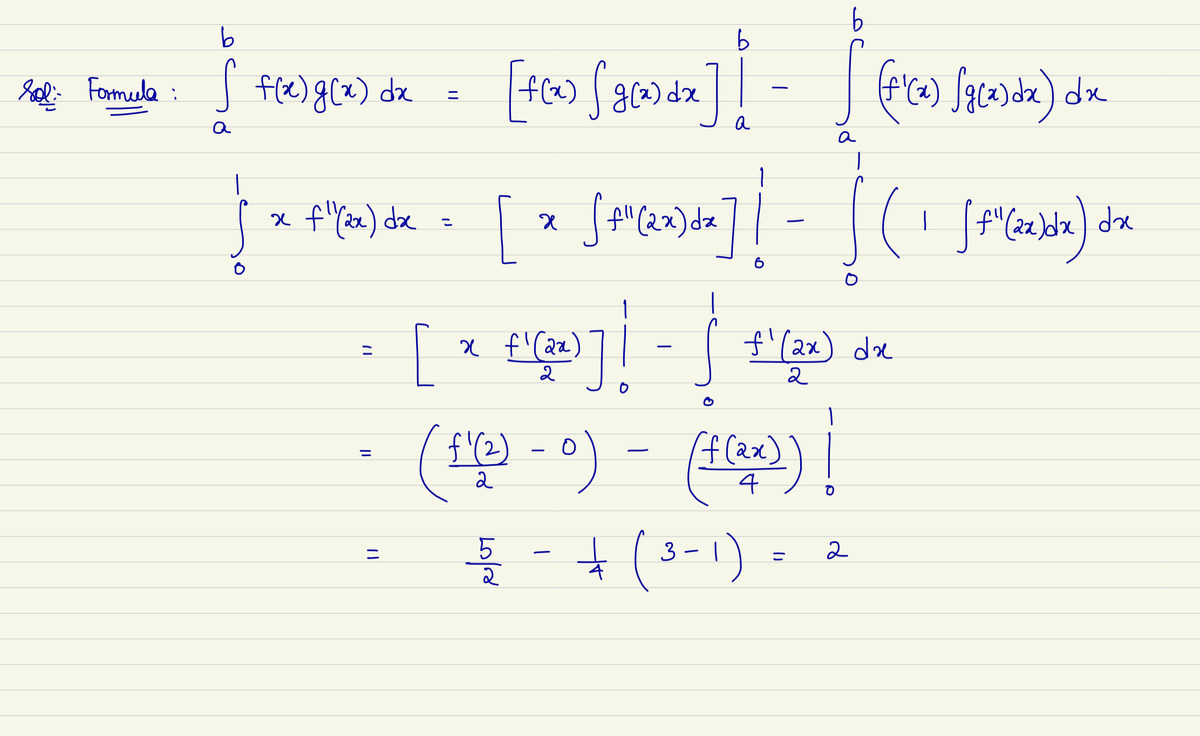
By integration by parts:
I = ∫ 0 1 x f ′ ′ ( 2 x ) d x = x ⋅ 2 1 f ′ ( 2 x ) ∣ ∣ ∣ ∣ 0 1 − ∫ 0 1 2 1 f ′ ( 2 x ) d x = 1 ⋅ 2 1 f ’ ( 2 ) − 0 − 4 1 f ( 2 x ) ∣ ∣ ∣ ∣ 0 1 = 2 5 − 4 1 ( f ( 2 ) − f ( 0 ) ) = 2 5 − 4 1 ( 3 − 1 ) = 2