Triangly-Circly Cone!!!
Note: This was a contest question hosted earlier by me, so don't get confused by the comments of the solutions posted in this problem.
Question:- In a circle. △ A B C is inscribed. Point P is on the interior of △ A B C such that it lies on the angle bisector of ∠ A B C . Also, the perpendicular segment drawn from Point P to side AC intersects the side AC at point D and the perpendicular segment drawn from Point P to side AB intersects the side AB at point E with seg PD = seg PE. One more thing is that points D and E are the midpoints of side AC and AB respectively. It is also given that seg DC= 3 units. Using the given information above, find the radius of the circle. See the diagram below for reference:
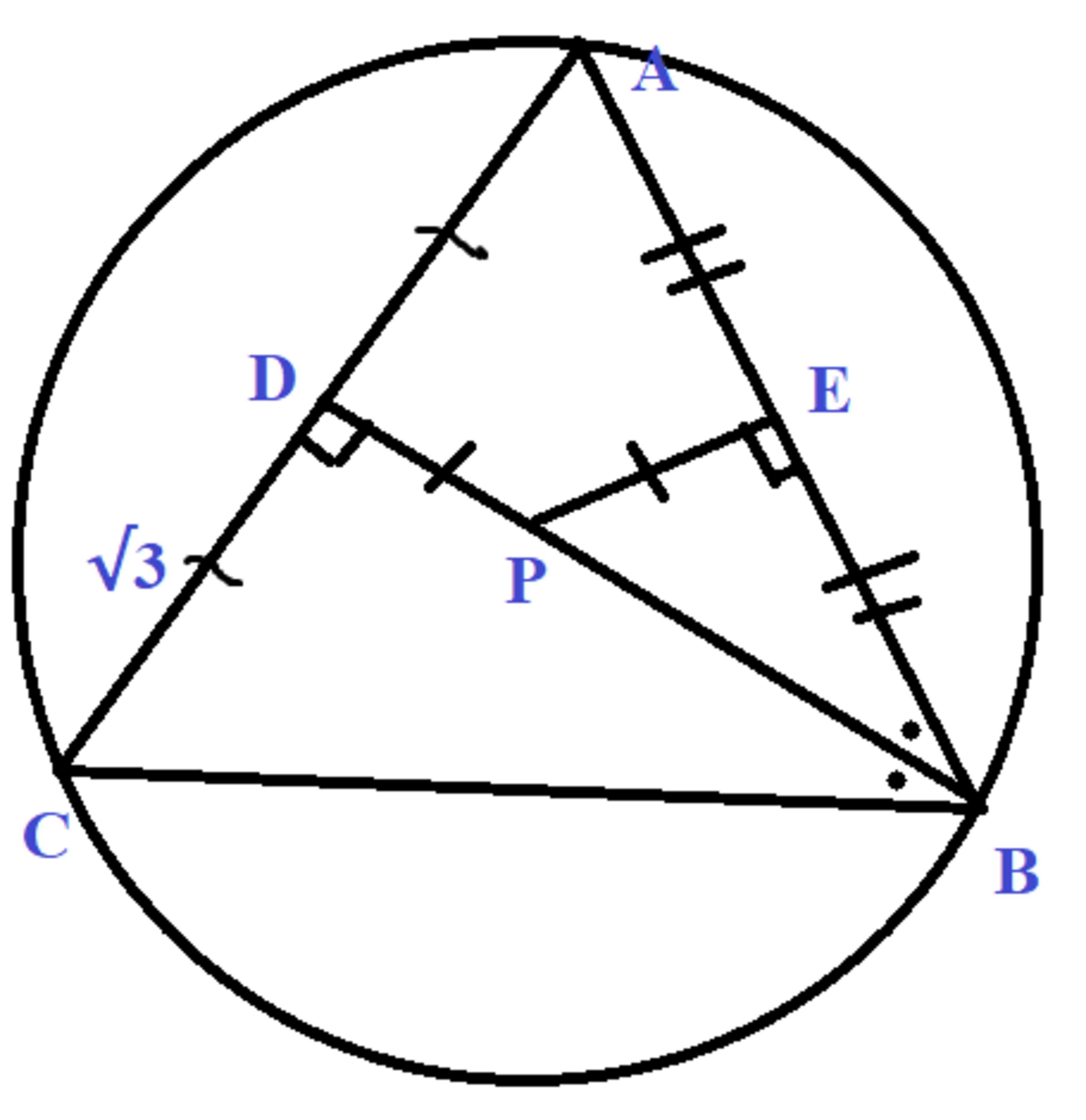 The image is not to scale
The image is not to scale
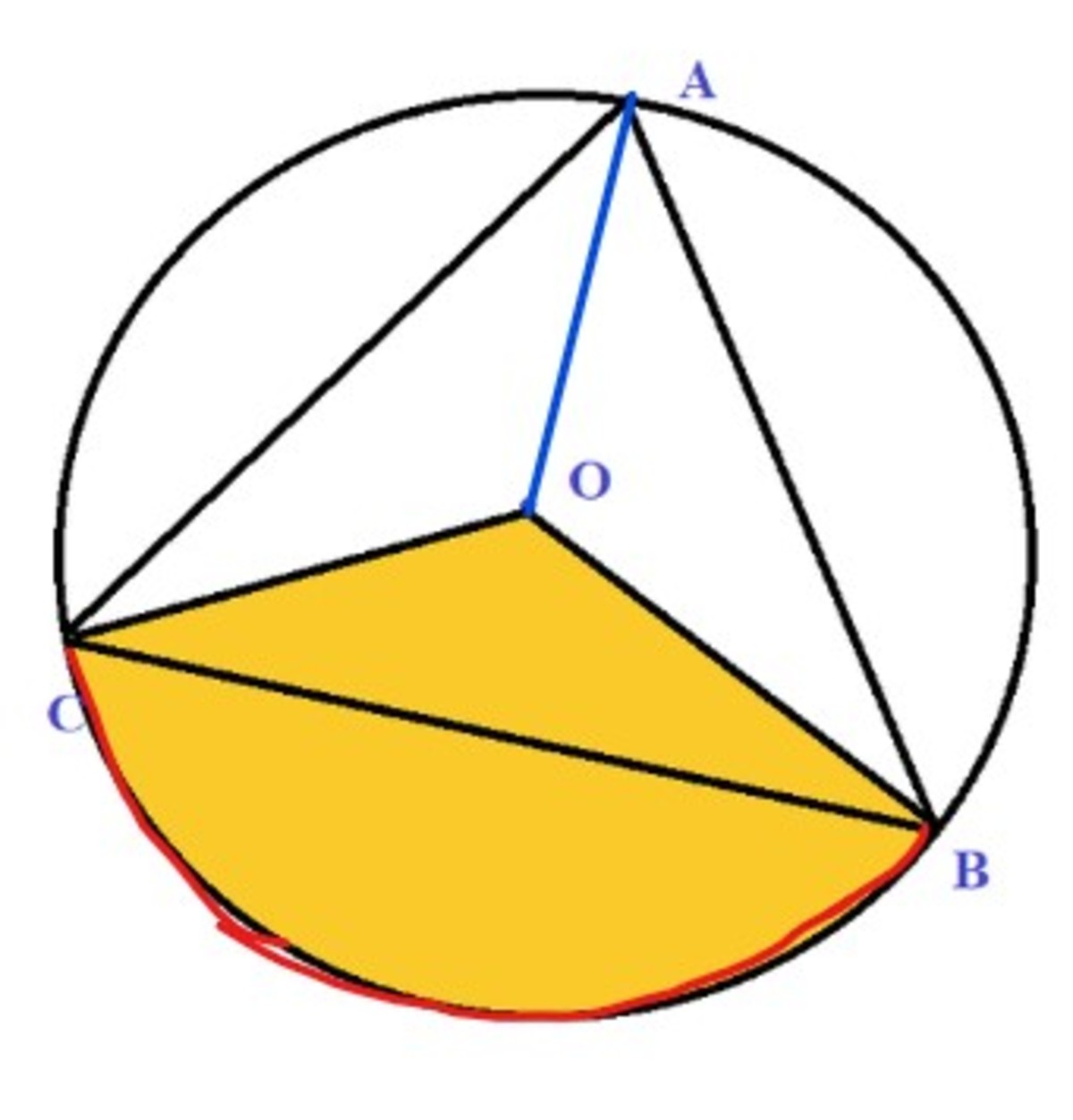
After finding the radius, with the centre of circle O lying on the interior of △ A B C , we join point O to point C and Point B, to get sector (OBC-O) as shaded below. We then cut out the sector (OBC-O) and wrap the sector around to form a cone. What is the height of the cone formed from the sector?
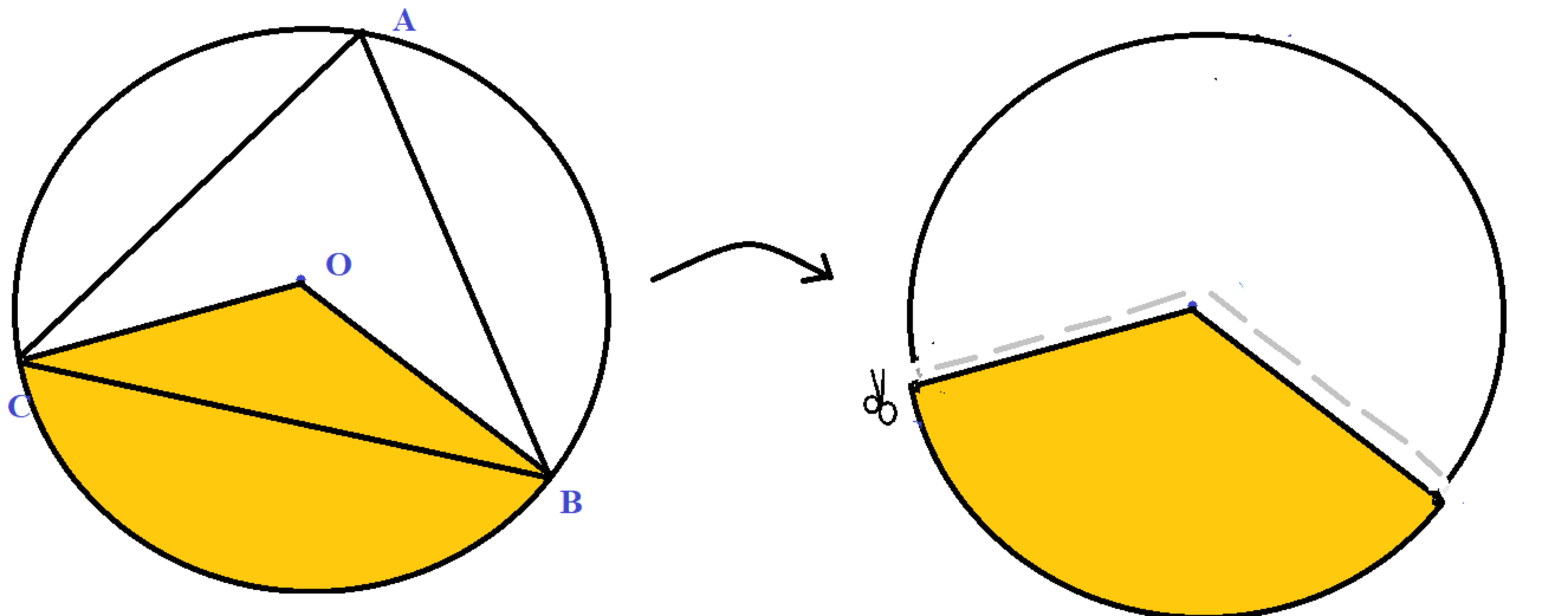 Sector(OBC-O) is cut out.
Sector(OBC-O) is cut out.
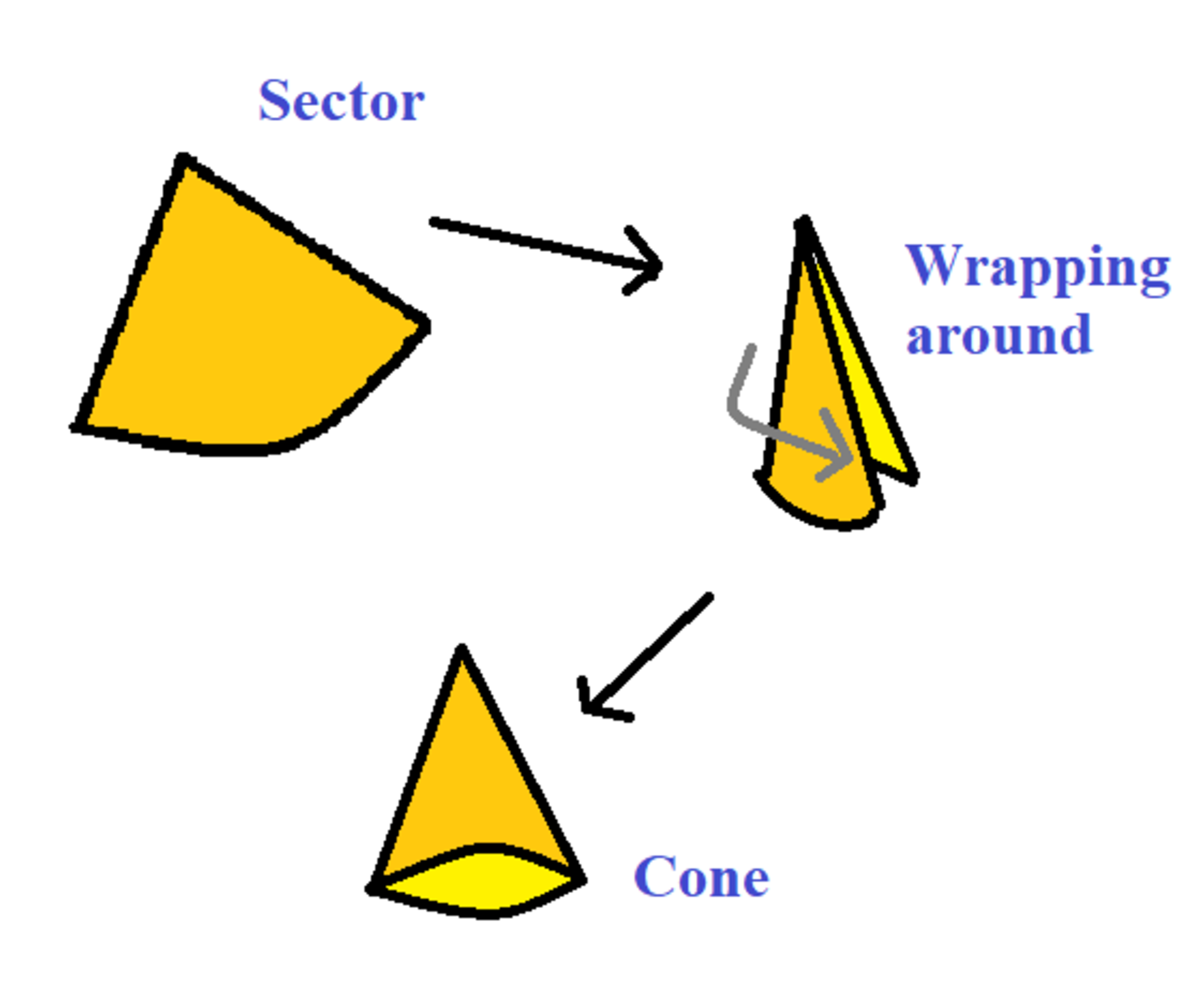 The sector is wrapped around to form a cone.
The sector is wrapped around to form a cone.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
radius is little greater than root 3 so it is 2 also height cannot be greater than slant height(radius) so this rules out 3rd option and the answer is 1st option
@Sahil Goyat, I would suggest to give the answer in a proper way without considering the options here. If the options were something else and all were convincing, you couldn't have answered then.
i know i should put this properly but i wanted to point that this question has options which make it unnecessary to actually solve it.
Triangle is equilater side 2*3^(1/2)
Base cone = long circle/3 => radius 2/3 => hight per pitagoras
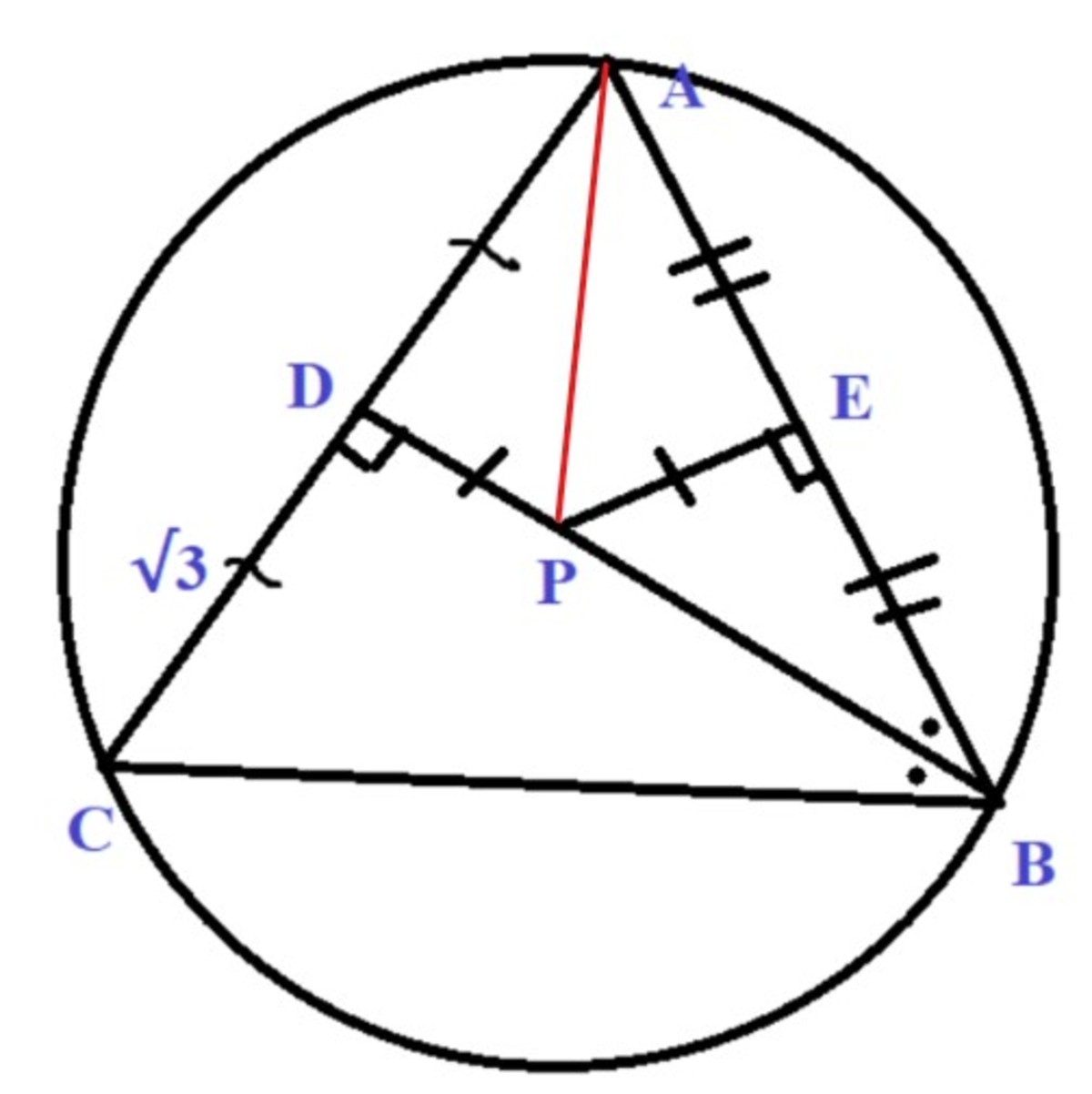
△ B D A ≅ △ B D C by ASA
- ∠ A B D = ∠ C B D (given)
- B D is the common line
- ∠ B D A = 9 0 ° = ∠ B D C
Hence, △ A B C is an isosceles triangle; B A = B C .
Draw a line joining A P ,
△ A P D ≅ △ A P E by RHS
- ∠ A D P = 9 0 ° = ∠ A E P
- A P is the common line
- P D = P E (given)
Thus, A D = A E and so A C = 2 3 = A B
Therefore, △ A B C is an equilateral triangle as three sides are equal length 2 3 .
Height of △ A B C = ( 2 3 ) 2 − ( 3 ) 2 = 3
As P is the centroid of △ A B C as well as the centre of the circle, radius A P = 3 2 × 3 = 2 Properties of centroid of a triangle
The centroid divides the equilateral triangle into 3 equal pieces.
Since we use 3 1 the circle to form a cone,
- the slant length of the cone = O C = 2
- the circumference of the base of the cone = 3 1 circumference of the original circle,
- thus, the radius R , of the cone's base circle = 3 1 × radius of the original circle = 3 1 × 2 = 3 2
Thus, the height of the cone = O C 2 − R 2 = 4 − 9 4 = 3 4 2
I am not sure to have time for all days in next week and making picture and animation is too time consuming. :)
Let the midpoint of B C be F and draw in P A , P C , and P F :
Since ∠ A D P = ∠ A E P = 9 0 ° , and since A P = A P by the reflexive property, and since we are given that D P = P E , then △ A D P ≅ △ A E P by the HL congruence theorem , and since corresponding parts of congruent triangles are congruent, A D = A E .
Since D P and E P are perpendicular bisectors of two chords A C and A B , P must be at the center of the circle.
Since P F goes through the center of the circle and bisects chord B C , ∠ P F B must be a right angle.
Since ∠ P F B = ∠ P E B = 9 0 ° , and since P B = P B by the reflexive property, and since we are given that ∠ P B F = ∠ P B E , then △ P F B ≅ △ P E B by the AAS congruence theorem , and since corresponding parts of congruent triangles are congruent, B F = B E .
Therefore, C D = D A = A E = E B = B F = F C = 3 , which means △ A B C is an equilateral triangle with a side length of 2 3 and a radius of r circle = 2 .
That means B C is one third the circumference of the original circle, or B C = 3 1 C circle = 3 1 ⋅ 2 π r circle = 3 1 ⋅ 2 π ⋅ 2 = 3 4 π . Since this length is the same length as the whole circumference of the base circle of the cone, C cone = 3 4 π , so the radius of the base circle of the cone is r cone = 2 π C cone = 2 π 3 4 π = 3 2 .
The slant height l of the cone is the same as the radius of the original circle, so l = r circle = 2 .
By the Pythagorean Theorem, the height h of the cone is h = l 2 − r cone 2 = 2 2 − ( 3 2 ) 2 = 3 4 2 .
Therefore, the radius of the original circle is 2 , and the height of the cone is 3 4 2 .