Un \text{Un} -Chebyshev Magic

Geometry Level 4

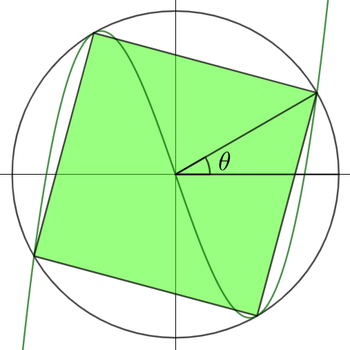
In the rectangular plane, the graph uniquely presented by the cubic polynomial function y = a 3 x 3 + a 2 x 2 + a 1 x + a 0 y = a_3x^3 + a_2x^2 + a_1x + a_0 passes through the square inscribed in a unit circle centered at the origin. There exists the rotation angle θ \theta of the vertex ( 1 , 0 ) (1,0) about the origin, such that the cubic equation passes through the circle exactly at 4 4 vertices.

If θ \theta can be expressed as A B π \dfrac{A}{B}\pi radians, where A , B A,B are coprime positive integers and 0 < A < 4 B 0 < A < 4B , input the product A B AB as your answer.


The answer is 6.

Michael Huang by Michael Huang , 29, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Mark Hennings
Apr 6, 2021

By symmetry, the cubic must be odd. Then the cubic y = a x 3 + b x y = ax^3 + bx passes through the points ( ± cos ⁡ θ , ± sin ⁡ θ ) (\pm \cos\theta, \pm\sin\theta) and ( ± sin ⁡ θ , ∓ cos ⁡ θ ) (\pm \sin\theta, \mp \cos\theta) , and the gradient of the cubic at the latter two points is tan ⁡ θ \tan\theta . Thus a cos ⁡ 3 θ + b cos ⁡ θ = sin ⁡ θ a sin ⁡ 3 θ + b sin ⁡ θ = − cos ⁡ θ 3 a sin ⁡ 2 θ + b = tan ⁡ θ a\cos^3\theta + b\cos\theta \; =\; \sin\theta \hspace{1cm} a\sin^3\theta + b\sin\theta \; =\; -\cos\theta \hspace{1cm} 3a\sin^2\theta + b \; = \; \tan\theta Thus we deduce that a = 1 sin ⁡ θ cos ⁡ θ ( cos ⁡ 2 θ − sin ⁡ 2 θ ) b = − cos ⁡ 4 θ + sin ⁡ 4 θ sin ⁡ θ cos ⁡ θ ( cos ⁡ 2 θ − sin ⁡ 2 θ ) a \; = \; \frac{1}{\sin\theta \cos\theta (\cos^2\theta - \sin^2\theta)} \hspace{2cm} b \; = \; - \frac{\cos^4\theta + \sin^4\theta}{\sin\theta \cos\theta(\cos^2\theta - \sin^2\theta)} and hence 3 sin ⁡ 2 θ sin ⁡ θ cos ⁡ θ ( cos ⁡ 2 θ − sin ⁡ 2 θ ) − cos ⁡ 4 θ + sin ⁡ 4 θ sin ⁡ θ cos ⁡ θ ( cos ⁡ 2 θ − sin ⁡ 2 θ ) = tan ⁡ θ 3 sin ⁡ 2 θ − cos ⁡ 4 θ − sin ⁡ 4 θ = sin ⁡ 2 θ ( cos ⁡ 2 θ − sin ⁡ 2 θ ) 3 tan ⁡ 2 θ ( 1 + tan ⁡ 2 θ ) − 1 − tan ⁡ 4 θ = tan ⁡ 2 θ ( 1 − tan ⁡ 2 θ ) 3 tan ⁡ 4 θ + 2 tan ⁡ 2 θ − 1 = 0 ( 3 tan ⁡ 2 θ − 1 ) ( tan ⁡ 2 θ + 1 ) = 0 \begin{aligned} \frac{3\sin^2\theta}{\sin\theta \cos\theta (\cos^2\theta - \sin^2\theta)} - \frac{\cos^4\theta + \sin^4\theta}{\sin\theta \cos\theta (\cos^2\theta - \sin^2\theta)} & = \; \tan\theta \\ 3\sin^2\theta - \cos^4\theta - \sin^4\theta & = \; \sin^2\theta(\cos^2\theta - \sin^2\theta) \\ 3\tan^2\theta(1 + \tan^2\theta) - 1 - \tan^4\theta & = \; \tan^2\theta(1 - \tan^2\theta) \\ 3\tan^4\theta + 2\tan^2\theta - 1 & = \; 0 \\ (3\tan^2\theta - 1)(\tan^2\theta + 1) & = \; 0 \end{aligned} so that tan ⁡ θ = 1 3 \tan\theta = \tfrac{1}{\sqrt{3}} , and hence θ = 1 6 π \theta = \tfrac16\pi , making the answer 1 × 6 = 6 1 \times 6 = \boxed{6} .

4 Helpful 3 Interesting 4 Brilliant 0 Confused

it's just beautiful, absolutely magical

Stolz Cesàro - 1 month, 4 weeks ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...