Thales' Triangle
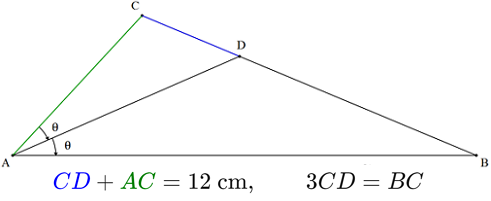
Given a triangle A B C , consider the bisector of ∡ A which intersects B C at the point D .
If C D + A C = 1 2 cm and C D = 3 B C , What is the perimeter of the triangle (in cm )?
The answer is 36.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
I'll be using standard conventions for Δ s in my solution.Let 2 A = X From the given data we see 3 a + b = 1 2 ⟹ a + 3 b = 3 6 . Also applying sin rule for Δ A D C we have 3 b sin ( X ) = A D sin ( C ) .Now applying sin rule for Δ A D B we have 3 2 b sin ( X ) = A D sin ( B ) . Now dividing one equation by the other we have sin ( C ) = 2 sin ( B ) ⟹ c = 2 b . The perimeter of Δ A B C β = a + b + c = a + b + 2 b = 3 6
As C D = 3 B C , we have A C + 3 B C = 1 2 c m
Now, B C C D = 3 1 ⟹ B C − C D C D = 3 − 1 1 ⟹ B D C D = 2 1 ⟹ A B A C = 2 1 The last equality follows by an application of angle bisector theorem .
Perimeter = A B + B C + C A = 2 ( A C ) + B C + A C = 3 ( A C + 3 B C ) = 3 ( 1 2 c m ) = 3 6 c m