What's with the hole?

Geometry Level 3

These two shapes seemingly have the "same" parts. What's the trick?

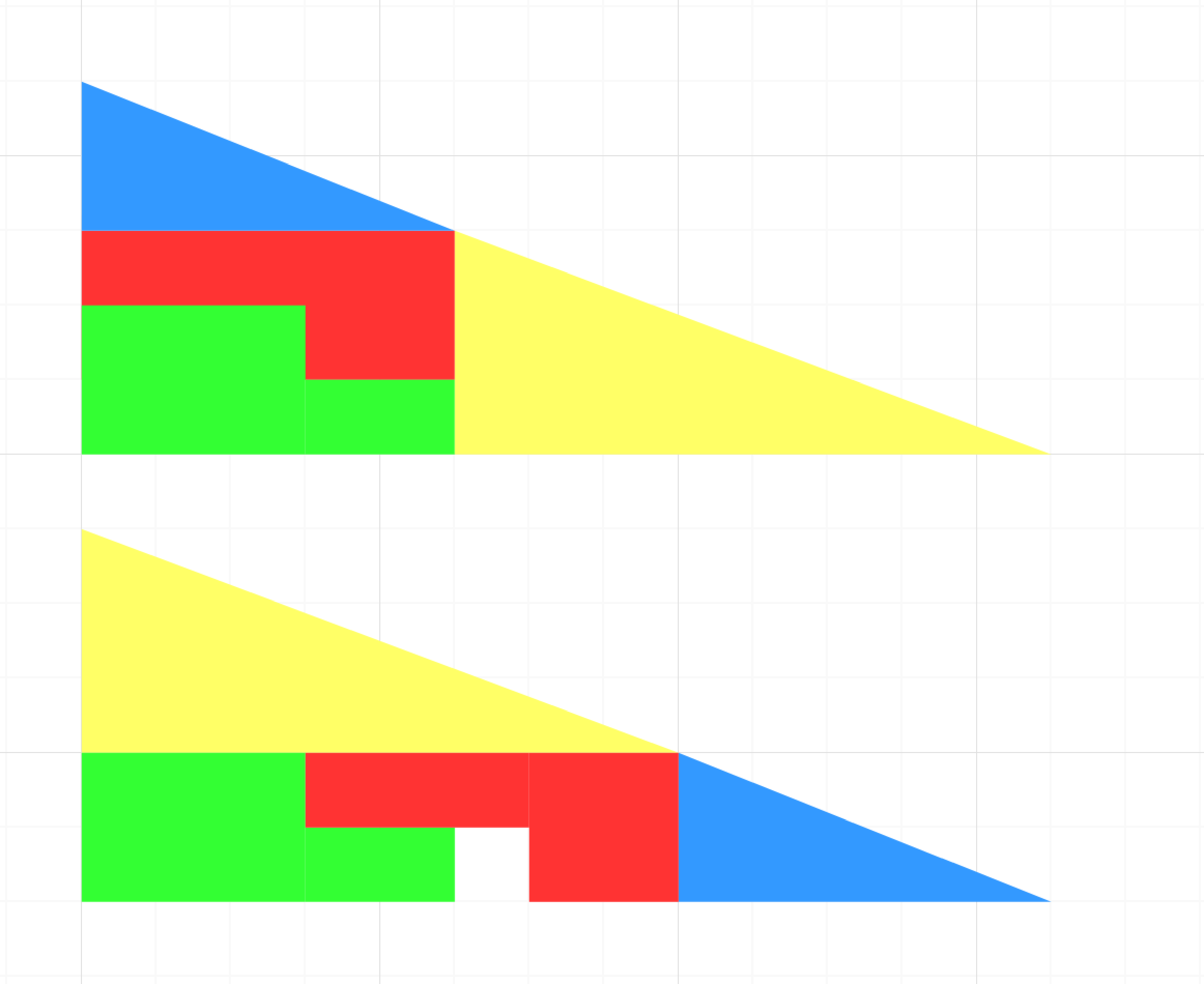
Source: Ripley's Believe It Or Not

The parts aren't the same. The pieces are slightly adjusted to make it look like they have right angles. The two legs of both shapes (assuming the hole was filled) do not form right angles. There is no trick, we were just misguided as kids. The length of their hypotenuses (assuming the hole was filled) aren't the same. They aren't triangles (assuming the hole was filled). The gridlines are skewed.

2 solutions

Marta Reece
Jul 15, 2017

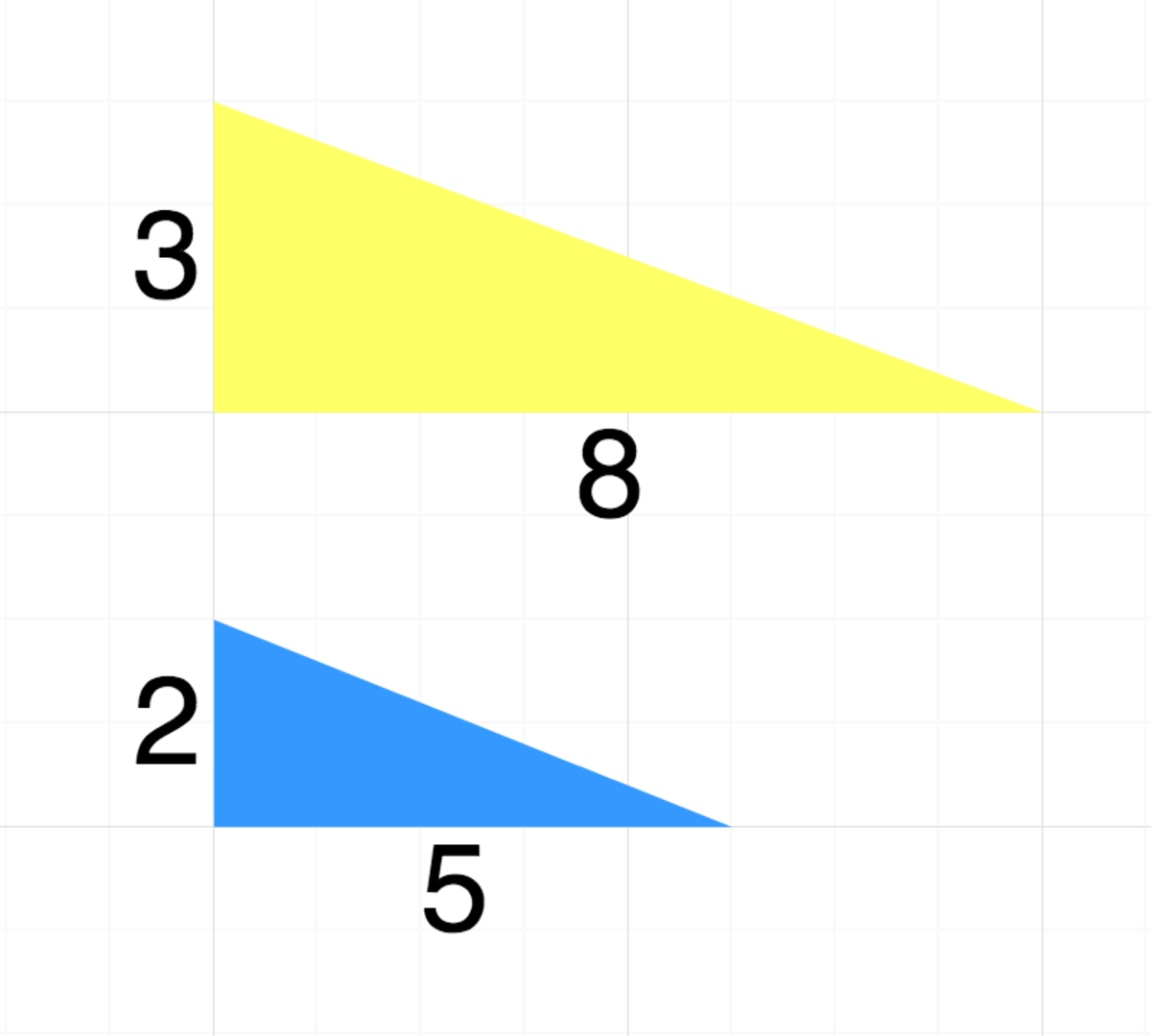
A straight line has been added for comparison. It seems to be only very slightly above and below the edge of the shape respectively, which explains the illusion. But the calculation below shows that this is enough.

The actual area of the colored “triangle” on top is

${\color{#3D99F6}\frac12\times2\times3}+{\color{#D61F06}3+2\times2}+{\color{#20A900}3\times2+2}+{\color{#CEBB00}\frac12\times3\times8}=32$

The area of the actual triangle would be

$\frac12\times5\times(5+8)=32.5$

And the area of the bottom colored “triangle” with the hole filled is

${\color{#3D99F6}\frac12\times2\times3}+{\color{#D61F06}3+2\times2}+{\color{#20A900}3\times2+2}+{\color{#CEBB00}\frac12\times3\times8}+1=33$

So the numbers bear it out.

Anthony Ling
Jul 15, 2017

If these shapes were triangles, the yellow and blue triangles would be similar to both of them. Therefore, the blue and yellow triangles would have the same side ratios. However, according to this figure:

They do not (since $\frac{3}{8}$ does not equal to $\frac{2}{5}$ ). Because of this, the overall shapes cannot be triangles (keep in mind that this does not prove why the hole exists, it only explains why this hole can appear).

What's with the hole?

2 solutions

0 pending reports