That is No Sierpinski Tetrahedron

Geometry Level 4

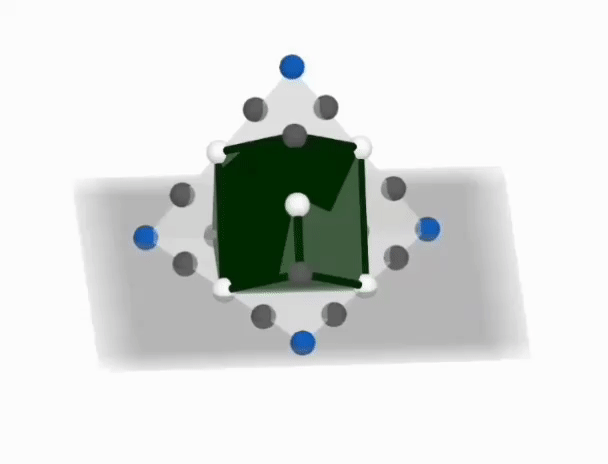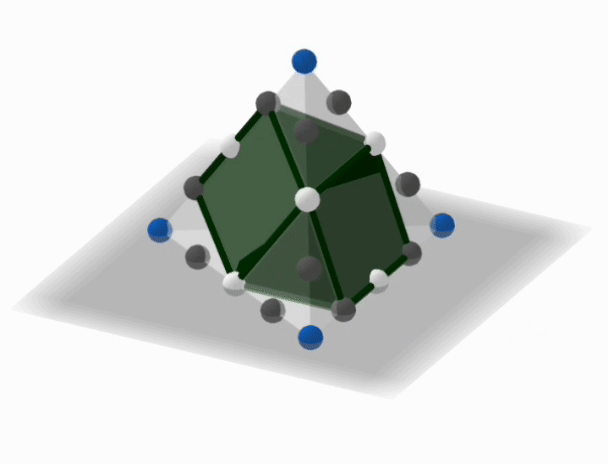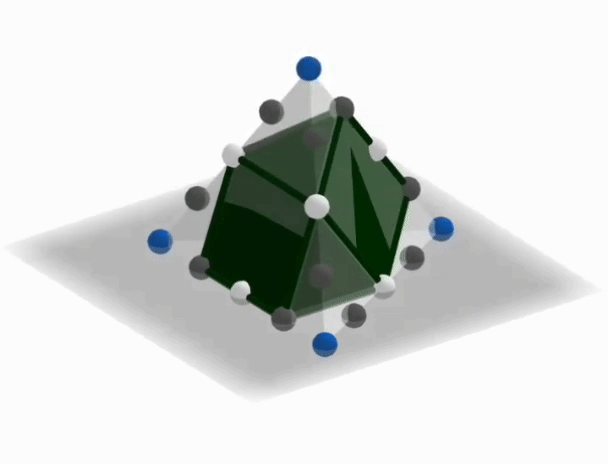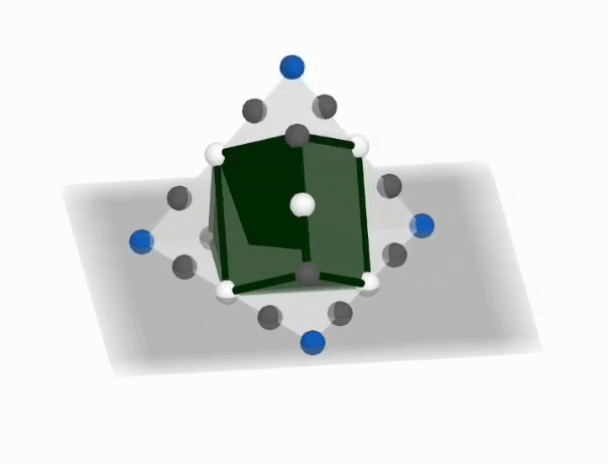
Three points quadrisect each edge of a regular tetrahedron--one white in the middle and two greys. As shown, the edge loop connects alternating points other than the vertices of the tetrahedron. Then, the green solid is formed by connecting six more edges of the same-colored midpoints.

If the volume of the green solid is $V_I=n V_B,$ where $V_B$ is the volume of the tetrahedron, what is the value of $n?$

\frac{2}{3}

\frac{3}{4}

\frac{4}{5}

\frac{5}{6}

\frac{7}{8}

None of the above

1 solution

Chew-Seong Cheong
Apr 18, 2018

Let the length between the blue vertex and white midpoint be 1, then the length between the vertices is 2. If the volume of the small tetrahedron of unit side length is $V$ then since volume of a similarly shaped solid is proportional to the cube of the side length then the volume of the large tetrahedron (side length 2) $V_B = 2^3 V = 8 V$ . Note that the volume of the inner solid is the volume of the large tetrahedron minus 4 halves of unit tetrahedron. Therefore,

$\begin{aligned} V_I & = V_B - 4 \times \frac 12 V \\ & = 8 V - 2 V = 6V \\ \implies V_I & = \frac 34 V_B \end{aligned}$

Therefore, $n = \boxed{\dfrac 34}$ .

That is No Sierpinski Tetrahedron

1 solution

0 pending reports