That Other Dodecahedron
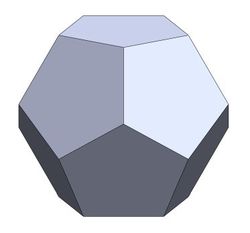 We're all familiar with the regular dodecahedron that has 12 identical flat regular pentagonal faces. If the edge length is 1, then the (area)² of each of those 12 faces is
But there is another dodecahedron that also has 12 identical flat pentagonal faces. If the edge length is 1 also, what is the (area)² of each of those 12 faces? If the answer is expressed as:
where a, b, c, d are irreducible positive integers, find
We're all familiar with the regular dodecahedron that has 12 identical flat regular pentagonal faces. If the edge length is 1, then the (area)² of each of those 12 faces is
But there is another dodecahedron that also has 12 identical flat pentagonal faces. If the edge length is 1 also, what is the (area)² of each of those 12 faces? If the answer is expressed as:
where a, b, c, d are irreducible positive integers, find
Those "12 identical flat pentagonal faces" need not be regular, but they must not intersect.
The answer is 28.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The polyhedron desired is called the Concave Pyritohedral Dodecahedron . Here is the image:
The faces are identical to the faces of a regular dodecahedron except for the fact that one pair of adjacent edges is concave, not convex. It is not hard to see that the area of a face of this shape is the area of the regular dodecahedron's face minus a b sin C where a = b = 1 and C = 1 0 8 ∘ . Evaluating gives 1 6 5 + 2 5 so our answer is 5 + 2 + 5 + 1 6 = 2 8 .