That unknown angle
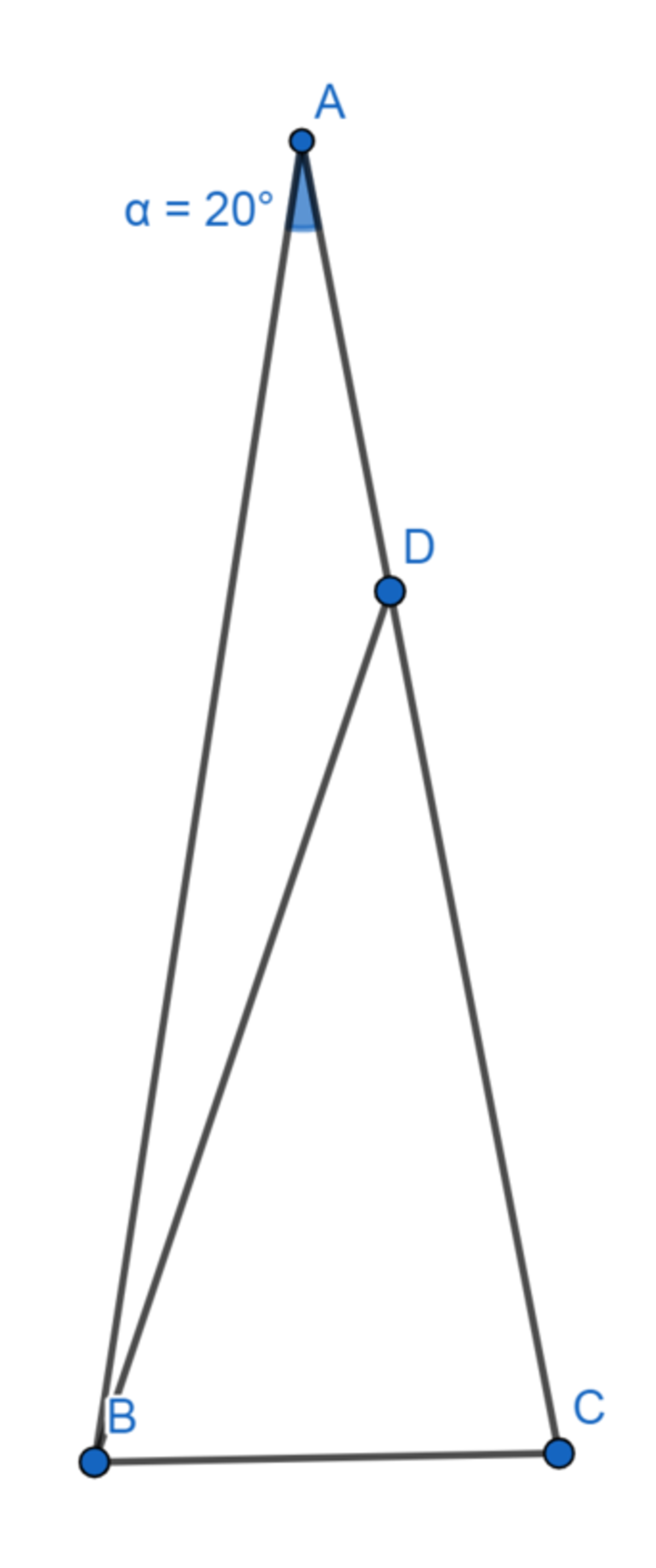
Let △ A B C be an isosceles triangle with A B = A C and ∠ A = 2 0 ∘ . Let D be a point on A C such that A D = B C . Find the measure of ∠ A B D in degrees.
Bonus : Solve it without using trigonometry or coordinate geometry.
This problem is not original.
The answer is 10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
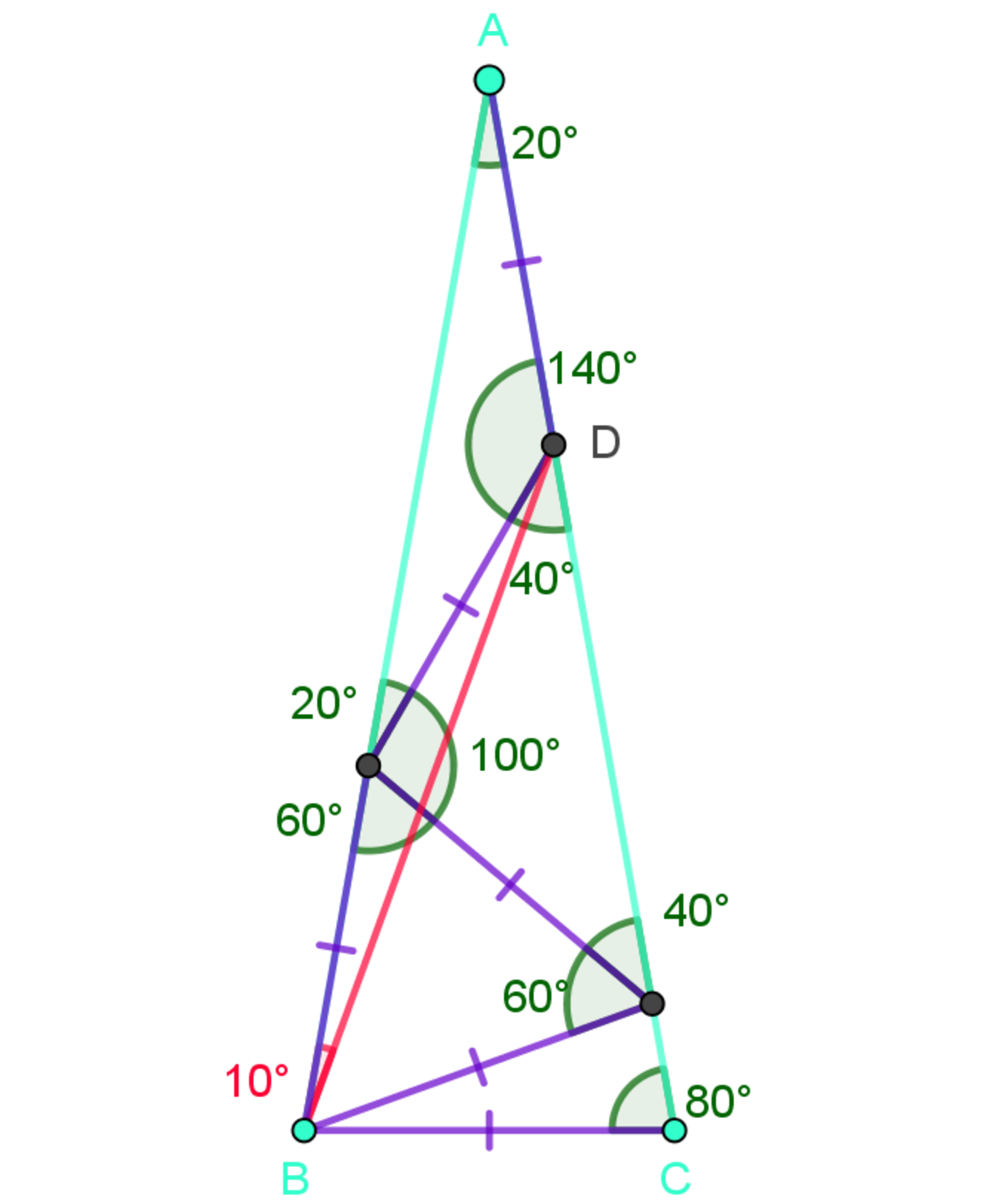
Hi, can you please describe the order in which you construct these congruent segments? I can't see why they are all congruent.
You do a zigzag from vertex A with segments of length BC until you reach the base. The angle measures confirm that it is doable.
I think this zigzag is possible for top vertex integer angle measures of: 4, 12, 20, 36, 60. In fact it is measures in the form of 2 n + 1 1 8 0 where n is natural number which is number of "zigzag segments".
Thank you for sharing this idea. It is very interesting! So, in our case n = 4 . You don't count the two segments which are on sides A B and A C , right? Does it have to do with the diagonals of regular polygons?
Log in to reply
It might have an interpretation relating diagonals of regular polygons, but i don't know one. The result can be derived by just drawing zigzag from the top vertex to the base and then repeatedly applying the exterior angle theorem.
Here is a simple proof : https://brilliant.org/discussions/thread/triangle-with-q-identical-lines/
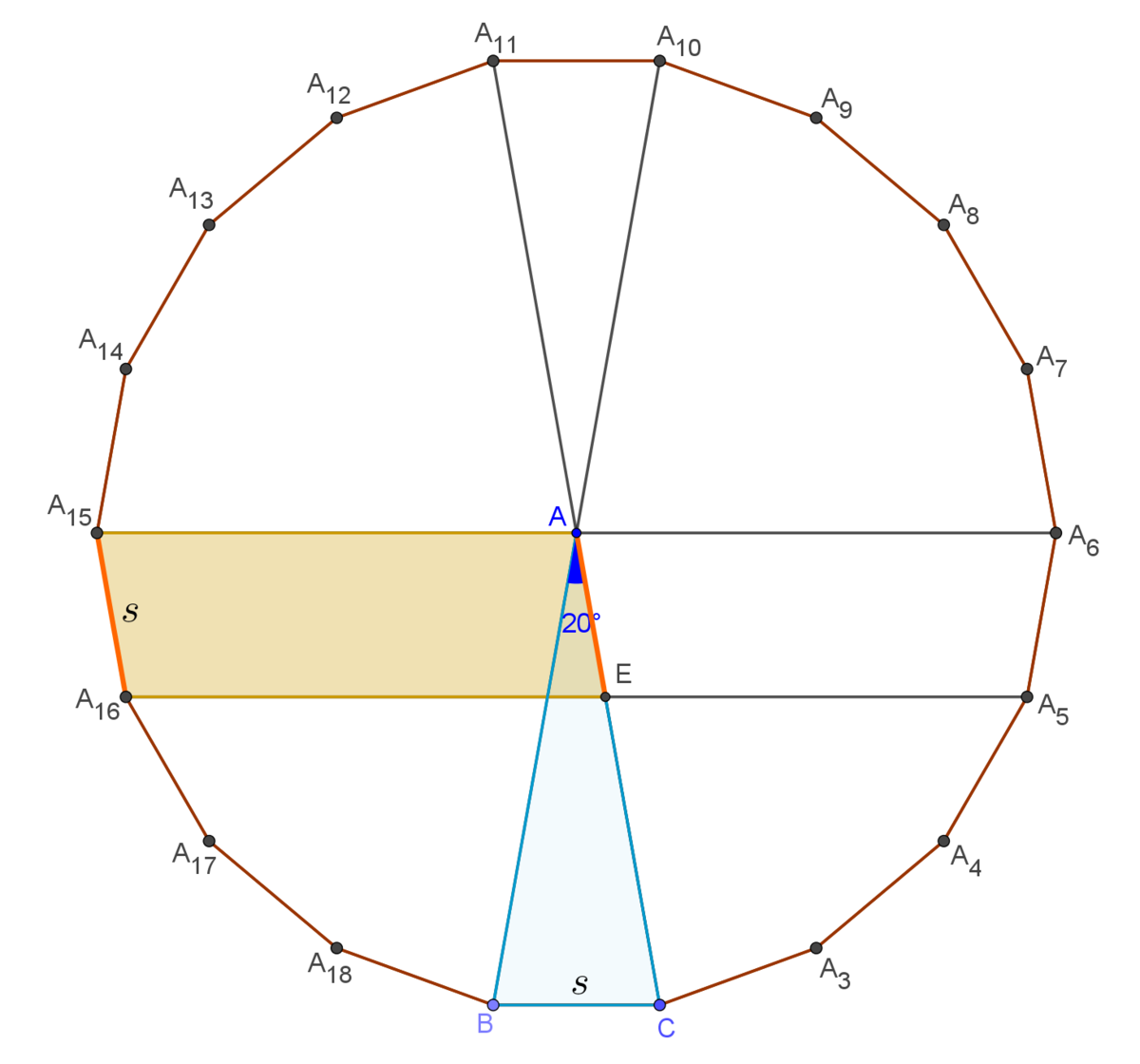 Figure 1
We first consider a regular 18-gon constructed on side
A
B
=
s
of
△
A
B
C
, having
A
as its circumcenter. Its vertices are labelled as seen on figure 1. We notice that diagonals
A
5
A
1
6
and
A
6
A
1
5
are parallel. Moreover, diagonal
C
A
1
1
is parallel to side
A
1
5
A
1
6
. Hence
A
E
A
1
6
A
1
5
is a parallelogram.
Figure 1
We first consider a regular 18-gon constructed on side
A
B
=
s
of
△
A
B
C
, having
A
as its circumcenter. Its vertices are labelled as seen on figure 1. We notice that diagonals
A
5
A
1
6
and
A
6
A
1
5
are parallel. Moreover, diagonal
C
A
1
1
is parallel to side
A
1
5
A
1
6
. Hence
A
E
A
1
6
A
1
5
is a parallelogram.
Thus,
A
E
=
A
1
5
A
1
6
(
1
)
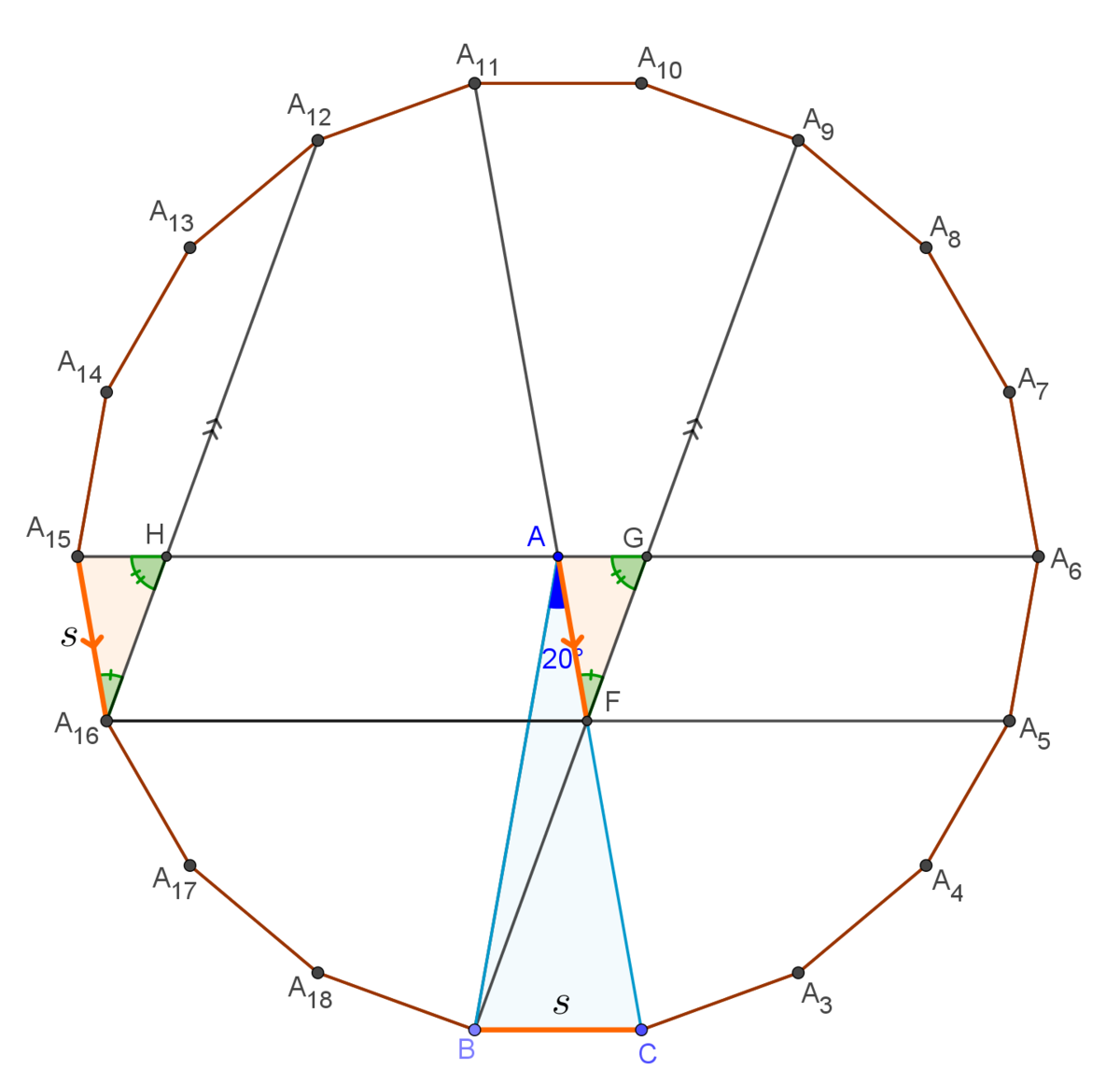 Figure 2
Figure 2
In figure 2, A 5 A 1 6 ∥ A 6 A 1 5 and A 1 2 A 1 6 ∥ A 9 B , hence G H A 1 2 F is a parallelogram, thus, G F = H A 1 6 .
Furthermore, due to pairs of parallel lines,
∠
G
F
A
=
∠
H
A
1
6
H
and
∠
F
G
A
=
∠
A
1
6
H
A
1
5
. Consequently, by ASA,
△
F
G
A
=
△
A
1
6
H
A
1
5
,
which gives that
A
F
=
A
1
5
A
1
6
=
s
(
2
)
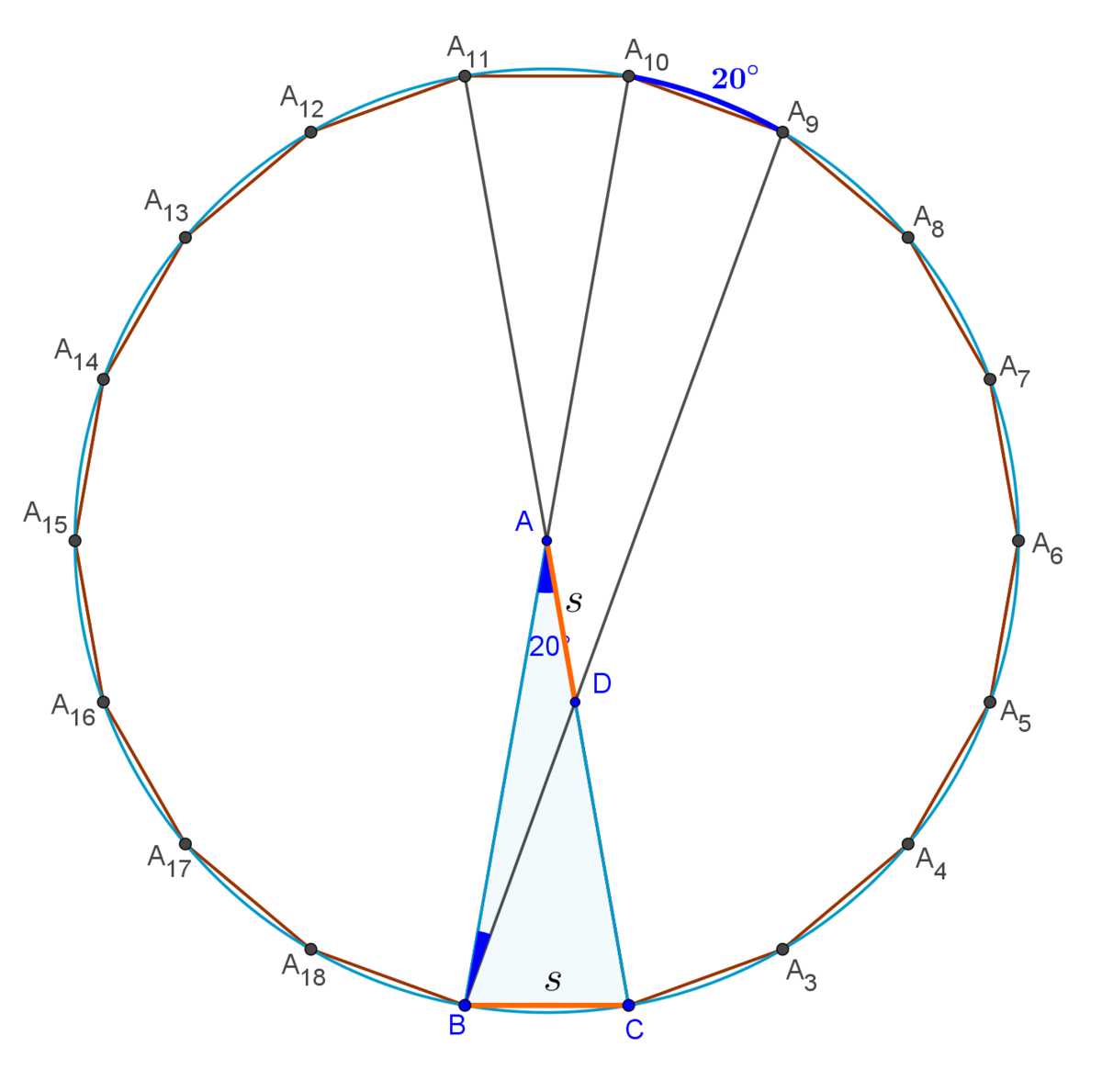 Figure 3
Figure 3
( 1 ) and ( 2 ) imply that both diagonals C A 1 1 and B A 9 intersect A C at the given point D (figure 3). Because of this, m ∠ A B D = 2 m A 9 A 1 0 ⌢ ⇒ ∠ A B D = 1 0 ∘ .
Let x = B D , and y = A D = B C and θ = ∠ A B D .
Noting that ∠ D C B = 8 0 ∘ , then by applying the Law of Sines to △ A B D and △ D B C , we get,
x sin 2 0 ∘ = y sin θ
and
x sin 8 0 ∘ = y sin ( 2 0 ∘ + θ )
Dividing the two equations out, yields,
sin 8 0 ∘ sin 2 0 ∘ = sin ( 2 0 ∘ + θ ) sin θ
Cross multiplying,
sin 2 0 ∘ sin ( 2 0 ∘ + θ ) = sin 8 0 ∘ sin θ
Using the identity sin ( A + B ) = sin A cos B + cos A sin B , the above equation becomes,
sin 2 0 ∘ ( sin 2 0 ∘ cos θ + cos 2 0 ∘ sin θ ) = sin 8 0 ∘ sin θ
Dividing through by cos θ , and collecting terms,
tan θ = sin 8 0 ∘ − sin 2 0 ∘ cos 2 0 ∘ sin 2 2 0 ∘ = 0 . 1 7 6 3 2 6 9 8 0 7 0 8 4
Therefore, θ = tan − 1 0 . 1 7 6 3 2 6 9 8 0 7 0 8 4 = 1 0 ∘
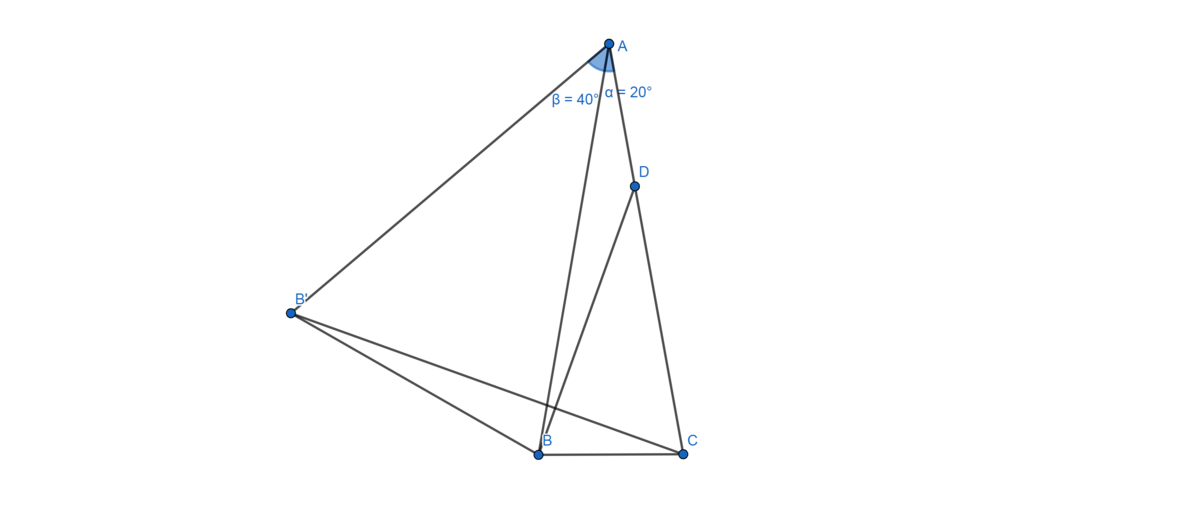
Rotate side A B 4 0 ∘ clockwise around point A such that B ends up in a new position B ′ . Draw B ′ C and B ′ B .
Observe that, in △ A B ′ C , A B ′ = A B = A C and ∠ B ′ A C = 4 0 + 2 0 = 6 0 ∘ , which indicates that △ A B ′ C is equilateral.
Also, observe that, in △ B ′ B C & △ D B A , B C = A D (given), B ′ C = A B ′ = A B & ∠ B ′ C B = ∠ A C B − ∠ A C B ′ = 8 0 − 6 0 = 2 0 ∘ = ∠ B A D .
⇒ △ B ′ B C ≅ △ B D A (By A − S − A criterion of congruence)
Hence, ∠ A B D = ∠ C B ′ B = ∠ A B ′ B − ∠ A B ′ C = 2 1 8 0 − 4 0 − 6 0 = 7 0 − 6 0 = 1 0 ∘ .