That's a lot of squares

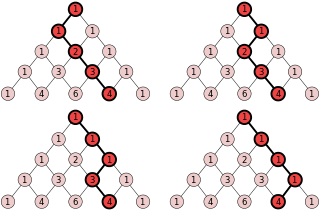
Consider two sets of $n$ objects. To choose $n$ of these objects, we can simply write this as $\binom{2n}{n}$ .

However, we may also consider including $0$ in what we choose from one group and excluding $0$ from the other group, including $1$ and excluding $1$ , etc. Thus, in total we have $\sum _{ j=0 }^{ n }{ {\binom{n}{j} }^{ 2 } }$ which must be equal to $\binom{2n}{n}$ .

As $n=100$ , the answer is $\binom{200}{100}$ so $m+n=300$ . (We may not write this number as a binomial coefficient so that $m+n$ is smaller)