That's A Pickle

Geometry Level 2

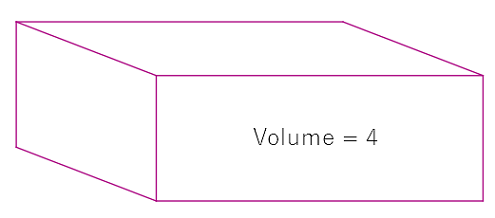
In a yard sale, there is this peculiar looking cuboid with a volume of 4.

I could have it for free if I'm able to find the product of all the 6 flat areas of the cuboid.

Am I able to determine the value of this product? If yes, what is its value?

256 No, it's not possible 128 512 64

Chung Kevin by Chung Kevin , 46, Australia

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Sam Bealing
May 8, 2016

Let the cuboid have sides lengths x , y , z x,y,z then the question tells us:

V o l u m e = x y z = 4 Volume=xyz=4

The six sides have areas x y , x y , y z , y z , x z , x z xy,xy,yz,yz,xz,xz and have product:

x y × x y × y z × y z × x z × x z = ( x y z ) 4 xy \times xy \times yz \times yz \times xz \times xz=(xyz)^4

So the answer is:

( x y z ) 4 = 4 4 = 256 (xyz)^4=4^4=\boxed{256}

3 Helpful 0 Interesting 0 Brilliant 0 Confused

Moderator note:

Good observation about the product of these areas :)

Thank you for your solution. It's surprising that we can find the relationship between the product of all the areas of the flat surface of the cuboid and the volume of the cuboid.

Chung Kevin - 5 years ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...