That's A Square
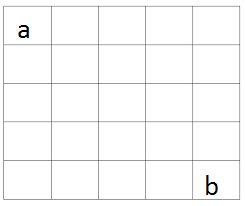
Given the following figure. if then find given that the number in the block is the arithmetic mean of the numbers in adjacent block.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Relevant wiki: Extremal Principle - Definition
Claim: In the event that a grid is filled with numbers in such a way that each entry is the average of all its surrounding entries, all the numbers on the grid are equal.
Proof: There must be some greatest number in the entire grid. But it must be the average of all its neighboring cells. Since we have assumed that this is the greatest number, the neighbors must either be smaller or equal to this number. But it cannot be smaller, since that contradicts the fact that our chosen square is the average of all these cells. So, they all must be equal to the original cell and one another. We can propagate this argument using induction to show that all the squares on the grid are equal.