That's a very narrow alley

Geometry Level 4

In an alleyway with tall buildings on both sides, a ladder of length 3.9 m 3.9 \text{ m} leans from the foot of the west wall on the east wall, while a ladder of length 2.5 m 2.5 \text{ m} leans the other way across the alleyway, from the foot of the east wall on to the west wall. Looking north along the alleyway, the ladders appear to cross 1 2 7 m 1\frac{2}{7} \text{ m} above the roadway.

How wide is the alleyway in metres? Round your answer to 3 decimal places


The answer is 1.500.

Sharky Kesa by Sharky Kesa , 19, United Kingdom

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

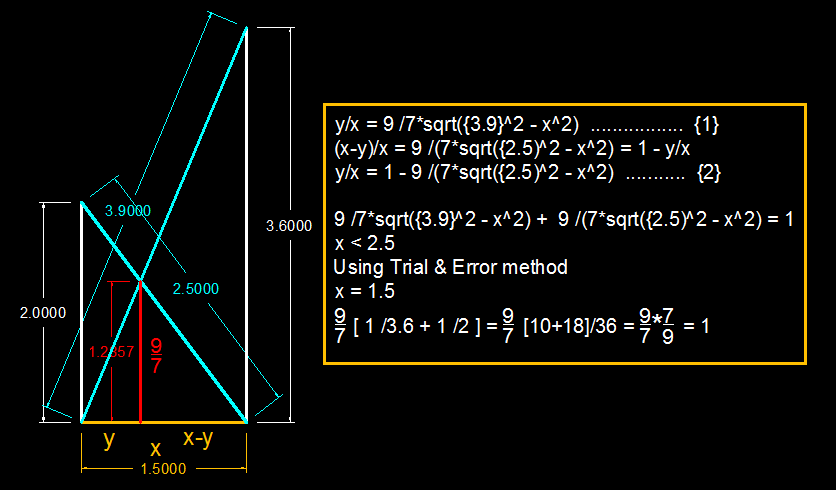
Crossed Ladder Formula applied,
1 d + 1 e = 7 / 9. B u t d = 2. 5 2 − x 2 , e = 3. 9 2 − x 2 . ∴ 2. 5 2 − x 2 + 3. 9 2 − x 2 = 7 9 ∗ 2. 5 2 − x 2 ∗ 3. 9 2 − x 2 S q u a r i n g b o t h s i d e t w i c e w i t h p r o p e r a d j u s t m e n t , f o r x > 0 , T h e r e s u l t i n g q u a d r a t i c i n x 2 g i v e s x = 15 \dfrac 1 d~+~\dfrac 1 e =7/9. \\ ~~~\\ But~d=\sqrt{2.5^2 - x^2},~~~~~~~e=\sqrt{3.9^2 - x^2}.\\ ~~~\\ \therefore~ \sqrt{2.5^2 - x^2}+ \sqrt{3.9^2 - x^2}\\ =\frac 7 9 * \sqrt{2.5^2 - x^2}* \sqrt{3.9^2 - x^2}\\ ~~~~~\\ Squaring ~both~side~twice~with~proper~adjustment,~~for~ x>0,\\ ~~~~\\ The ~resulting~ quadratic~ in ~x^2~gives~x=\color{#D61F06}{\Large 15 }

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Ahmad Saad
May 29, 2016

0 Helpful 0 Interesting 0 Brilliant 0 Confused

Can you give a solution which doesn't use trial and error please? We want to make sure this is the only solution after all.

Sharky Kesa - 5 years ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...