That's A Weird Frame
A conducting frame is composed by joining the curves and the line .
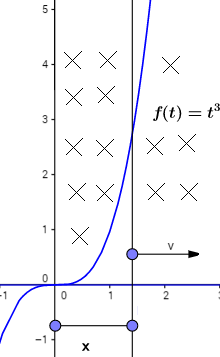
The conducting frame has 0 resistance. A uniform magnetic field of magnitude Tesla is directed inwards as shown. A magical conducting rod parallel to -axis starts moving from the origin along the positive direction of -axis with intial velocity .
This magical rod has special properties as follows:
1) It has a finite mass .
2) Its resistance per unit length varies as where is the distance of the rod from the origin.
If the distance travelled by the rod till it comes to rest is
Find
Details :
Take .
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
When the rod is at a distance x metres from the origin moving with velocity v, the area of the loop is,
∣ A ∣ = ∫ 0 x z 3 d z
The magnetic flux through the loop ϕ = B ⋅ A = ∣ B ∣ ∣ A ∣ cos 0 = B ⋅ ∫ 0 x z 3 d z
According to Faraday's laws an EMF is induced in the coil, E = − d t d ϕ = − B x 3 d t d x = − B x 3 v V
The instantaneous current through the coil, I = R E = σ x 3 − B x 3 v = σ 0 ( 1 + x 4 ) − B v A
A current carrying conductor moving in a magnetic field experiences a force,
F = i l B
F = σ 0 ( 1 + x 4 ) − B v ⋅ x 3 ⋅ B = σ 0 ( 1 + x 4 ) − B 2 v x 3 N
m a = σ 0 ( 1 + x 4 ) − B 2 v x 3
v d x d v = m σ 0 ( 1 + x 4 ) − B 2 v x 3
− d v = m σ 0 ( 1 + x 4 ) B 2 x 3 d x
∫ u 0 − d v = ∫ 0 L 4 m σ 0 ( 1 + x 4 ) B 2 4 x 3 d x
u = 4 m σ 0 B 2 ⋅ [ ln ( 1 + x 4 ) ] 0 L = 4 m σ 0 B 2 ⋅ ln ( 1 + L 4 )
∴ L 4 = e B 2 4 m σ 0 u − 1
∴ L = ⎝ ⎛ e B 2 4 m σ 0 u − 1 ⎠ ⎞ 4 1
⌊ L ⌋ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎝ ⎛ e B 2 4 m σ 0 u − 1 ⎠ ⎞ 4 1 ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥
Substituting the values
∴ ⌊ L ⌋ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎝ ⎛ e 1 2 4 ⋅ 1 ⋅ 1 ⋅ 2 − 1 ⎠ ⎞ 4 1 ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥
∴ ⌊ L ⌋ = ⎣ ⎢ ⎢ ⎢ ( e 8 − 1 ) 4 1 ⎦ ⎥ ⎥ ⎥ = ⎣ ⎢ ⎢ ⎢ ( e 8 ) 4 1 ⎦ ⎥ ⎥ ⎥ = ⌊ e 2 ⌋
∴ ⌊ L ⌋ = ⌊ 7 . 3 8 9 ⌋ = 7