That's all?

Geometry Level 2

The two larger angles of an isosceles triangle have a combined measure of $135^\circ$ . If this triangle has a perpendicular height of $2\text{ m}$ , find the length of its base in meters.

If the latter can be expressed in the form $a\sqrt { b } -c$ , where $a,b$ and $c$ are positive integers with $b$ square-free, write your answer as $a\times b\times c$ .

The answer is 32.

3 solutions

Niranjan Khanderia
Jun 9, 2016

Vertex angle is 180 - 135=45.
If the base is X whose length we are to find, then, $\dfrac X 2=(perpendicular\ \ height )*Tan\frac 1 2\!*\!45.\\$
$\implies\ X=2*(2)*\left(\dfrac{Sin45}{1+Cos45} \right ) = 4*\left(\dfrac{\dfrac 1 {\sqrt2}}{1+\dfrac 1 {\sqrt2}} \right ) = 4*\left(\dfrac{(\dfrac 1 {\sqrt2})*(1 - \dfrac 1 {\sqrt2})}{1- \dfrac 1 2} \right )\\ =4*(\sqrt2 - 1)=4*\sqrt2 - 4=a\sqrt b - c.\\ So\ a*b*c=4*2*4=32.$

The large angles could be 45 and 90, rather than 67.5 degrees. This would make a triangle with two 45 degree angle and 90 at the vertex, with base equal 4. (Or if you were to take a different view, base could be 2. "Perpendicular height" need not be from the vertex at 90 degrees.)

Marta Reece - 4 years, 5 months ago

Jonas Katona
Jun 9, 2016

Since the angles in a triangle must add up to $180°$ , the last angle must be $45°$ ( $180°-135°=45°$ ). Also, since the two other angles besides this $45°$ angle are larger than the latter, they must both measure at $\frac { 135° }{ 2 } =67.5°$ . This is because two angles in an isosceles triangle must be the same measure, and since both are larger than $45°$ , both must be of the same measure, and thus are each half of $135°$ .

From here, the perpendicular height in an isosceles triangle is actually the measure of the altitude from the vertex with a unique angle (that is, a measure unlike any other vertex in the triangle). Due to the symmetry in an isosceles triangle, this perpendicular height splits this angle right in half and will also connect directly to the center of the base across.

Since this resultant line is perpendicular, it splits the isosceles triangle into two right triangles. 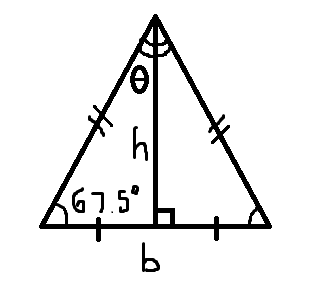Analyzing the angle which was split in half by the height, one can write an equation using tangent: $\tan { \theta =\frac { { b }/{ 2 } }{ h } }$ Noting that $\theta =\frac { 45° }{ 2 } =22.5°$ , we can now plug in variables and solve for the base.

Using the half-angle formula for tangent, $\tan { \frac { \alpha }{ 2 } } =\frac { 1-\cos { \alpha } }{ \sin { \alpha } }$ , where in this case, $\alpha =45°$ , $\tan { 22.5°=\frac { { b }/{ 2 } }{ 2m } }$ $\sqrt { 2 } -1=\frac { { b }/{ 2 } }{ 2m } =\frac { b }{ 4m }$ $b=4m\left( \sqrt { 2 } -1 \right) =\left( 4\sqrt { 2 } -4 \right) m=\left( a\sqrt { b } -c \right) m$

Putting this into the form of the answer, $a=4,b=2,c=4$ , so $a\times b\times c=4\times 2\times 4=\boxed { 32 }$ .

You should include how to find the exact value of $\tan {22.5°}$ in your solution, as it is not trivial.

Alex G - 5 years ago

Well, I honestly just had it memorized (it is the inverse of the silver ratio), but one could use the half-angle formula for tangent. I just included that, thank you!

Jonas Katona - 5 years ago

A Former Brilliant Member
Jun 9, 2016

The length of the base in metres is $\frac{4}{\tan 67.5^\circ}=\frac{4}{\sqrt{2}+1}=4\sqrt{2}-4$ . Hence the answer is 32.

Can anyone show how to solve this without using trignometry.... Also experts can you help me out with some really interesting resources links for olympiads for grades 6, 7 and 8. Thanks in advance !!!!

Shankara Narayanan - 4 years, 7 months ago

Area of triangle ABC= 0.5 b b sin45
Also area of triangle ABC = 0.5* 2*a
Cos 45= (b^2 +b^2 -a^2)/2 b b Hence a= 4{(2)^0.5}-4 Where a- base of isosceles triangle b- two equal sides of triangle

Rn munjal - 2 years, 5 months ago

That's all?

The answer is 32.

3 solutions

0 pending reports