That's an Ugly Looking Octagon
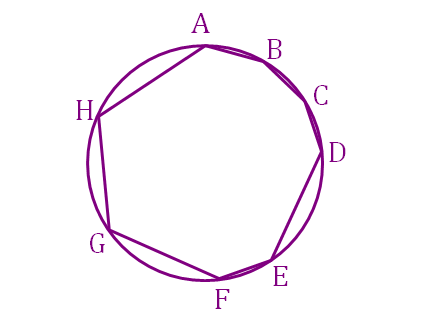
As shown in the diagram above, A B C D E F G H is an inscribed octagon where A B = B C = C D = E F = 1 and D E = F G = G H = H A = 2 .
If the area of the octagon can be expressed as a + b c , where a , b , c are all integers and c is square-free, then find the value of a + b + c .
The answer is 11.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Of course! Why didn't I think of that! (-:
Very nice construction. I think it is worth justifying why the "new octagon is simply a square with 4 of its corners cut off".
∠ H A ′ B ′ will be 135
Log in to reply
Whoops XP what a stupid mistake, my bad. I've updated the solution.
First time managed to solve a geometry question without pen n paper. Yay!
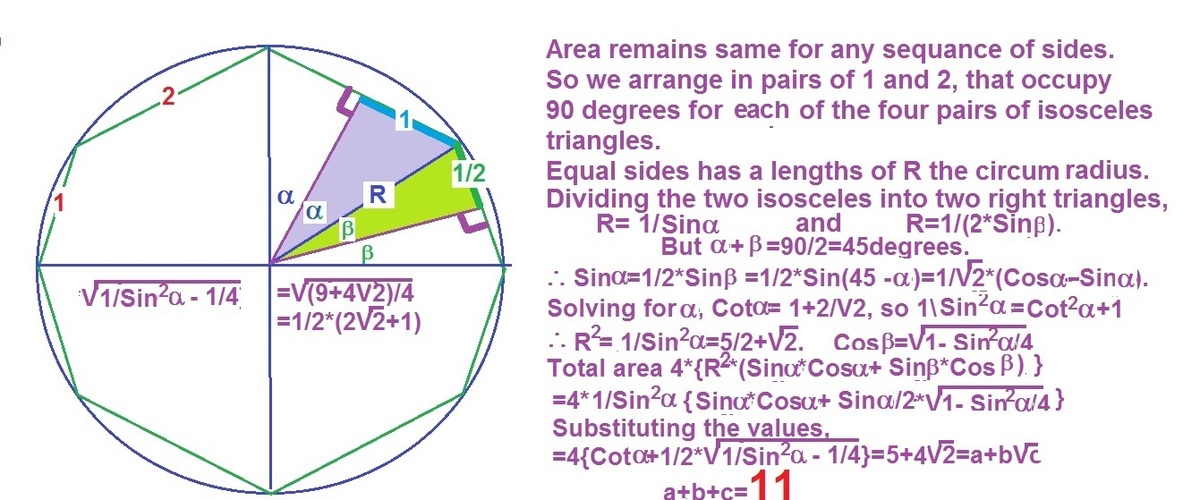
Let O be the centre of the circle and r be the radius of the circle.
The area would be unchanged if the sides were alternating (1, 2, 1, 2, etc). This means ∠ EOG = 90 ∘ .
Let ∠ GOF = θ . Then ∠ EOF = 90 - θ .
The cosine rule ( a 2 = b 2 + c 2 − 2 b c cos A ) on GOF and EOF respectively gives:
4 = 2 r 2 − 2 r 2 cos θ
1 = 2 r 2 − 2 r 2 cos ( 9 0 − θ ) 1
Noting that cos ( 9 0 − θ ) = sin θ , rearranging these gives:
2 r 2 = 1 − cos θ 4
2 r 2 = 1 − sin θ 1
Setting the RHSs of these equal and multiplying out the denominators gives:
4 − 4 sin θ = 1 − cos θ
4 sin θ − 3 = cos θ
4 sin θ − 3 = 1 − sin 2 θ
Squaring both sides leads to the quadratic in sin θ :
1 7 sin 2 θ − 2 4 sin θ + 8 = 0
So sin θ = 1 7 1 2 + 2 2 2 .
sin 2 + cos 2 = 1 gives cos θ = 1 7 − 3 + 8 2 3 .
Now the area required is equivalent to 4 times the area of OEFG.
Area = 4 ( 2 1 r 2 sin θ + 2 1 r 2 sin ( 9 0 − θ ) )
Area = 4 ( 2 1 r 2 sin θ + 2 1 r 2 cos θ )
Area = 2 r 2 ( sin θ + cos θ )
Substituting using equation 1 ,
Area = 1 − sin θ 1 ( sin θ + cos θ )
Using surd forms (equations 2 and 3 ) ultimately simplifies to:
Area = 5 + 4 2 .
So a + b + c = 5 + 4 + 2 = 1 1 .
Surely there's a simpler approach!?
I also used the same approach. It was a bit lengthy. But the intuition used in the first solution by @Tan Kenneth is really interesting.
I used this method as well, was blown away by @Tan Kenneth 's solution!
my original.
Using the beautiful concept of Tan Kenneth.
The first thing we need to figure out is how do we transform this ugly octagon into plain beauty!
Imagine cutting the octagon into pieces from the centre to the vertices and labelling them from 1 to 8, like this: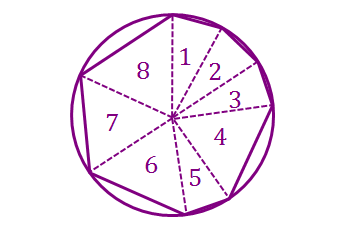 Now rearrange the pieces so that it becomes:
Now rearrange the pieces so that it becomes:
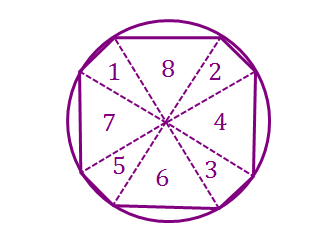 That's much better. Since rearranging the pieces doesn't change its area, we can calculate the area of the original octagon by calculating the area of this new octagon.
That's much better. Since rearranging the pieces doesn't change its area, we can calculate the area of the original octagon by calculating the area of this new octagon.
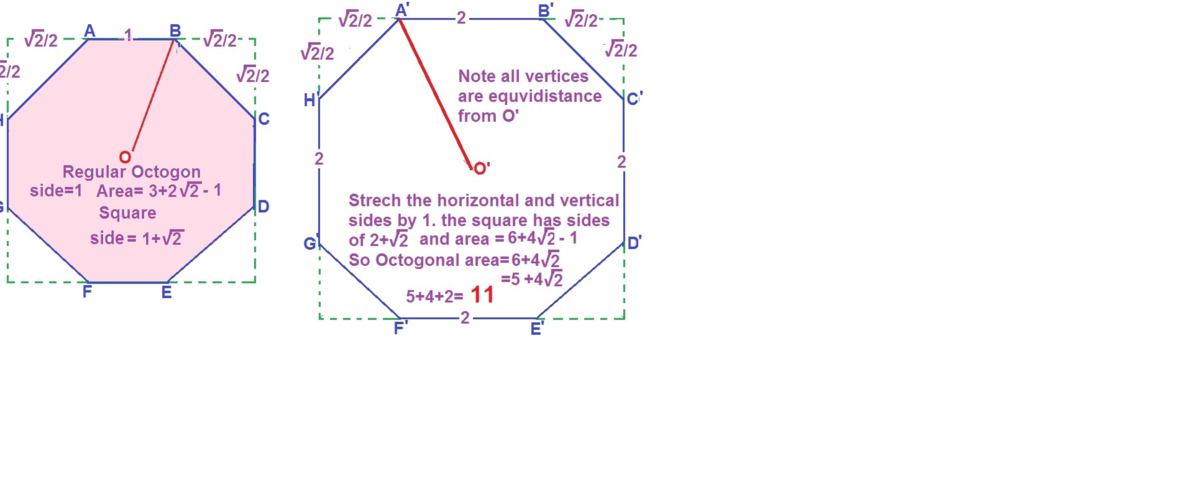
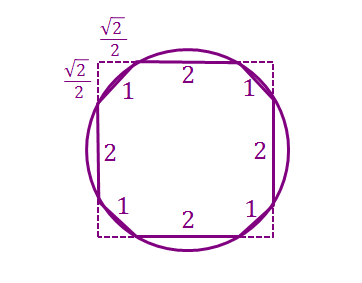 Notice that the new octagon is simply a square with 4 of its corners cut off, the cut off corners are all congruent right isosceles triangles (to see why, read the supplementary notes below), thus, using a bit of Pythagoras' theorem, denoting
S
a shape
as the area of a shape, we can easily figure out that the area of this octagon is
S
square
−
4
S
right isosceles triangle
=
(
2
+
2
)
2
−
4
×
2
1
×
(
2
2
)
2
=
6
+
4
2
−
1
=
5
+
4
2
Hence,
a
=
5
,
b
=
4
,
c
=
2
,
a
+
b
+
c
=
1
1
.
Notice that the new octagon is simply a square with 4 of its corners cut off, the cut off corners are all congruent right isosceles triangles (to see why, read the supplementary notes below), thus, using a bit of Pythagoras' theorem, denoting
S
a shape
as the area of a shape, we can easily figure out that the area of this octagon is
S
square
−
4
S
right isosceles triangle
=
(
2
+
2
)
2
−
4
×
2
1
×
(
2
2
)
2
=
6
+
4
2
−
1
=
5
+
4
2
Hence,
a
=
5
,
b
=
4
,
c
=
2
,
a
+
b
+
c
=
1
1
.