That's not how you make ice cream

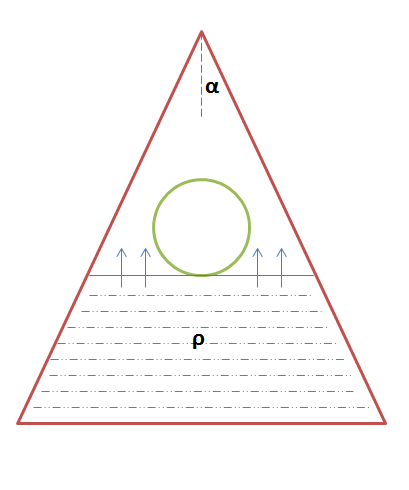A sphere of negligible mass and radius $r = 1 \text{ cm}$ is placed inside a smooth hollow cone with semi-vertical angle $\alpha = \dfrac{\pi}{6}$ .

Then, a liquid of density $\rho = 1000 \text{ kg/m}^{3}$ rises into the cone until no more liquid can possibly enter.

If the normal reaction force per unit length $N_\lambda$ between the sphere and the walls of the cone can be expressed in SI units as $\frac{a\sqrt{b}}{c}$ where $a$ , $b$ and $c$ are natural numbers with $b$ square free and $a$ and $c$ coprime, what is the value of $a+b+c$ ?

Details and Assumptions :

• Assume that the sphere forms a tight seal with the walls of the cone and prevents the liquid from rising further

• A small hole is present at the vertex of the cone to allow air to escape

• Take $g = 10 \text{m/s}^2$ .