That's our childhood
A boy is initially seated on the top of a hemispherical
mound of radius
R
as shown in the figure.
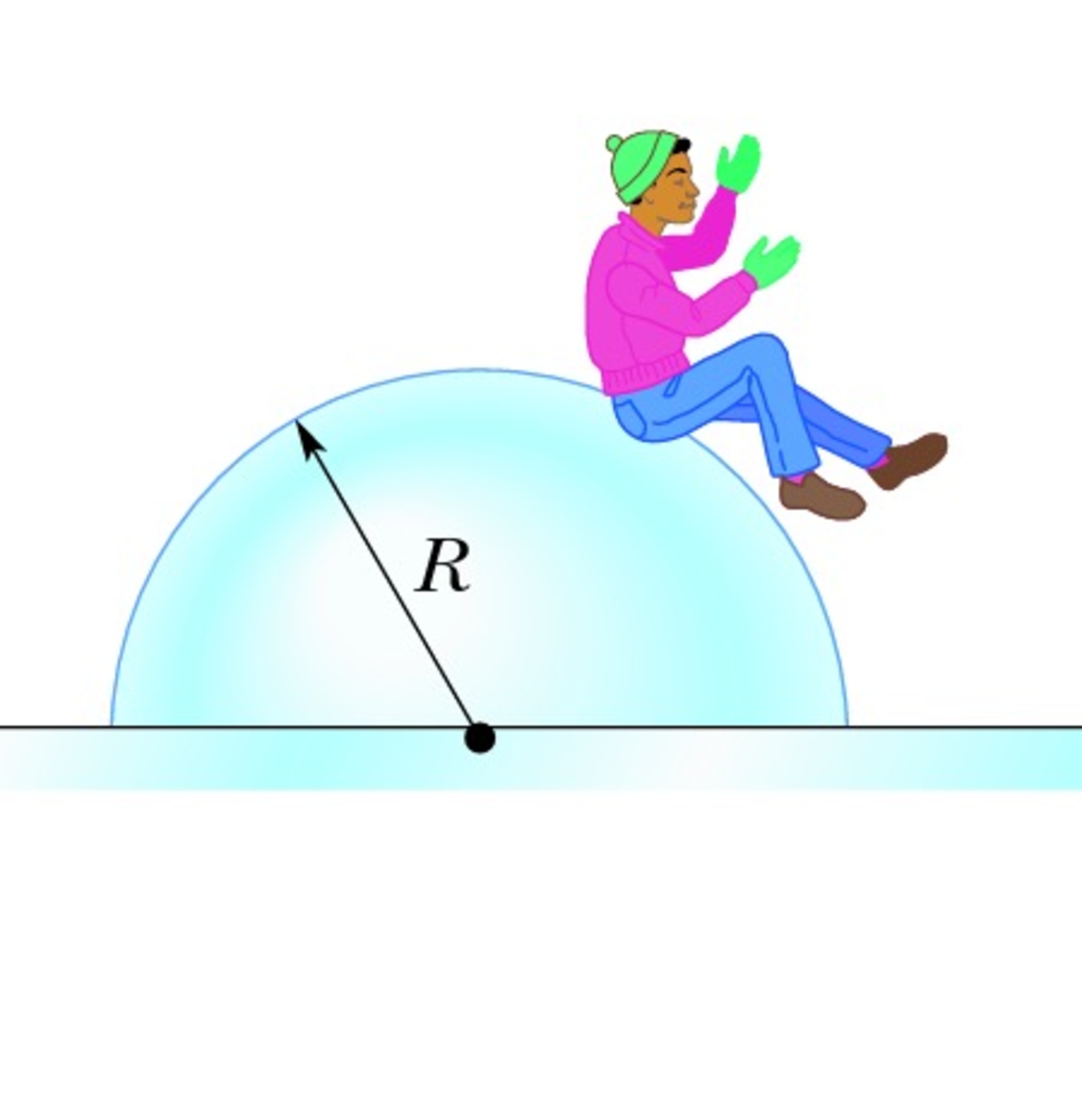
He begins to slide down the ice, with a negligible initial speed.At what height(in m) does the boy loose contact with the ice ?
Details :
- Radius of hemispherical mound is 13.8 m .
- Approximate the ice as being frictionless.
The answer is 9.20.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the boy lose contact at point (R,theta). No energy lost due to friction, hence at highest spot(R,0), E =mgR + 0, while at point(R, theta), E = mgRsin(theta) + 1/2mv^2 Hence mgR(1-sin(theta)) = 1/2 mv^2 and v^2 = 2gR(1-sin(theta))
Next, when the boy loses contact, it is because required centripetal force > supplied centripetal force. F required = mv^2/R F supplied = mgsin(theta) - Fn, Fn is the support force acting on the boy, and since mgsin(theta) decreases, support force must decrease until 0, which the boy then loses contact. So at (R,theta) Fn = 0 , mv^2/R = mgsin(theta) and v^2 = gRsin(theta)
Hence, 2gRsin(1-sin(theta)) = gRsin(theta) We get 2-2sin(theta) = sin(theta) and sin(theta) = 2/3
so height h = Rsin(theta) = 13.8*2/3 = 9.2(m)