That's why I like physics
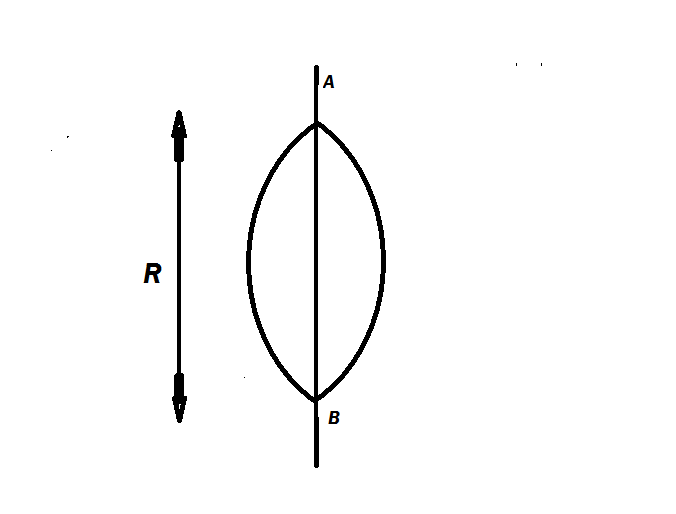
Two portions of a thin ring each of mass M and and radii R are joined together as as shown. Find the moment of inertia of the system about axis AB.
If it can be expressed as M R 2 × ( c − π d 3 ) ÷ 2 , find c + d .
The answer is 14.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
I lost my points as I got trapped in that 'divided by 2' in the answer form that is written in the question...: (
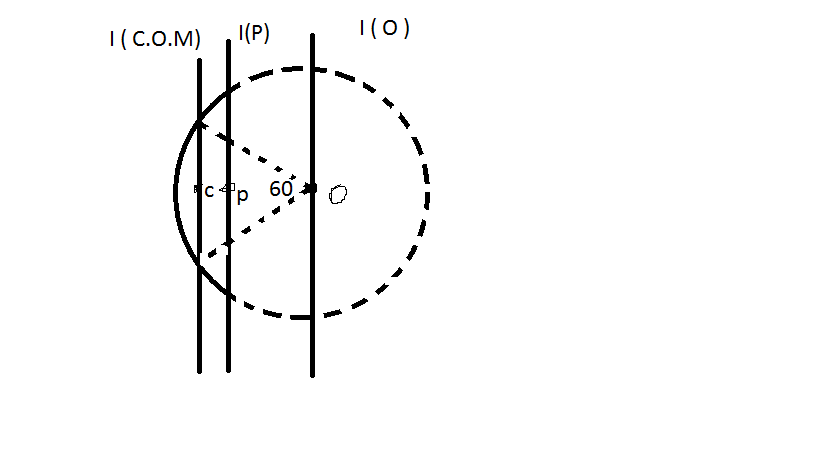
Sorry , I would not be able to post the whole solution but the sol. will surely answer the question asked
In the given fig . "c" is centre of mass of the portion of the ring. O is centre of the ring and we need to calculate "I(P)"
You can calculate it using the method to calculate that of a semicircular ring and it comes out to be - π 3 R = OC
I (O) - M(OC )^2 = I(C.O.M) ... Using parallel axis theorem .
I (P) = I (C.O.M) + M(CP)^2
where cp = oc - op = π 3 R - 3 2 R
( OP is calculated using trignometry)
Now , since both portions are similar ,
Net Moment of Inertia = 2 * I(P)
giving c = 5 and d = 9
Answer = 1 4
I apologize if something is missing or unclear .
i would add a shortcut to calculate com. if you remember it for half ring then divide it into 3 parts equal and let it's cm be at distance x let mass=m(each part)
{mx+mxsin(30)+mx(sin30)}/3m=2R/pi
x=3R/pi
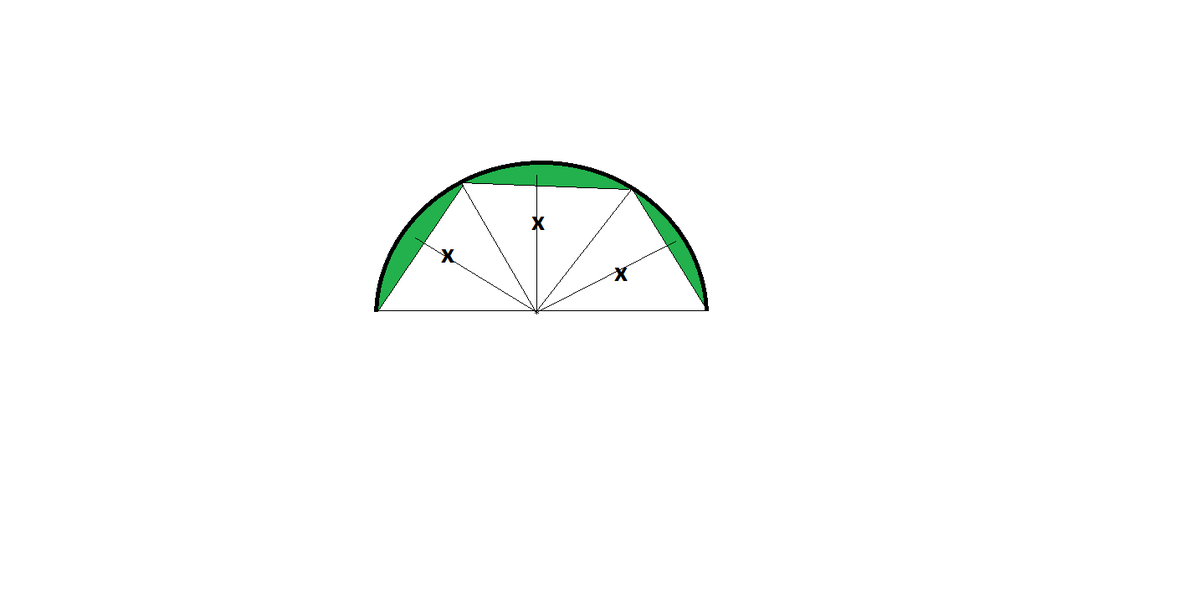
The points where the ring segments meet are distance R apart, so the angle of reach segment is 60° or 3 π radians.
Moment of inertia L = ∫ r 2 d m .
Note:
L = 4 ∫ 0 6 π R 2 ( cos φ − cos 6 π ) 2 π 3 M d φ
= π 1 2 R 2 M ∫ 0 6 π cos 2 φ − 3 cos φ + 4 3 d φ
= π 1 2 R 2 M ∫ 0 6 π 2 1 cos 2 φ + 2 1 − 3 cos φ + 4 3 d φ
= π 1 2 R 2 M ( 4 1 sin 3 π + 1 2 π − 3 sin 6 π + 4 3 6 π )
= π 1 2 R 2 M ( 2 4 5 π − 8 3 3 )
= 2 R 2 M ( 5 − π 9 3 )
5 + 9 = 1 4