The 3 Wisemen

Geometry Level 4

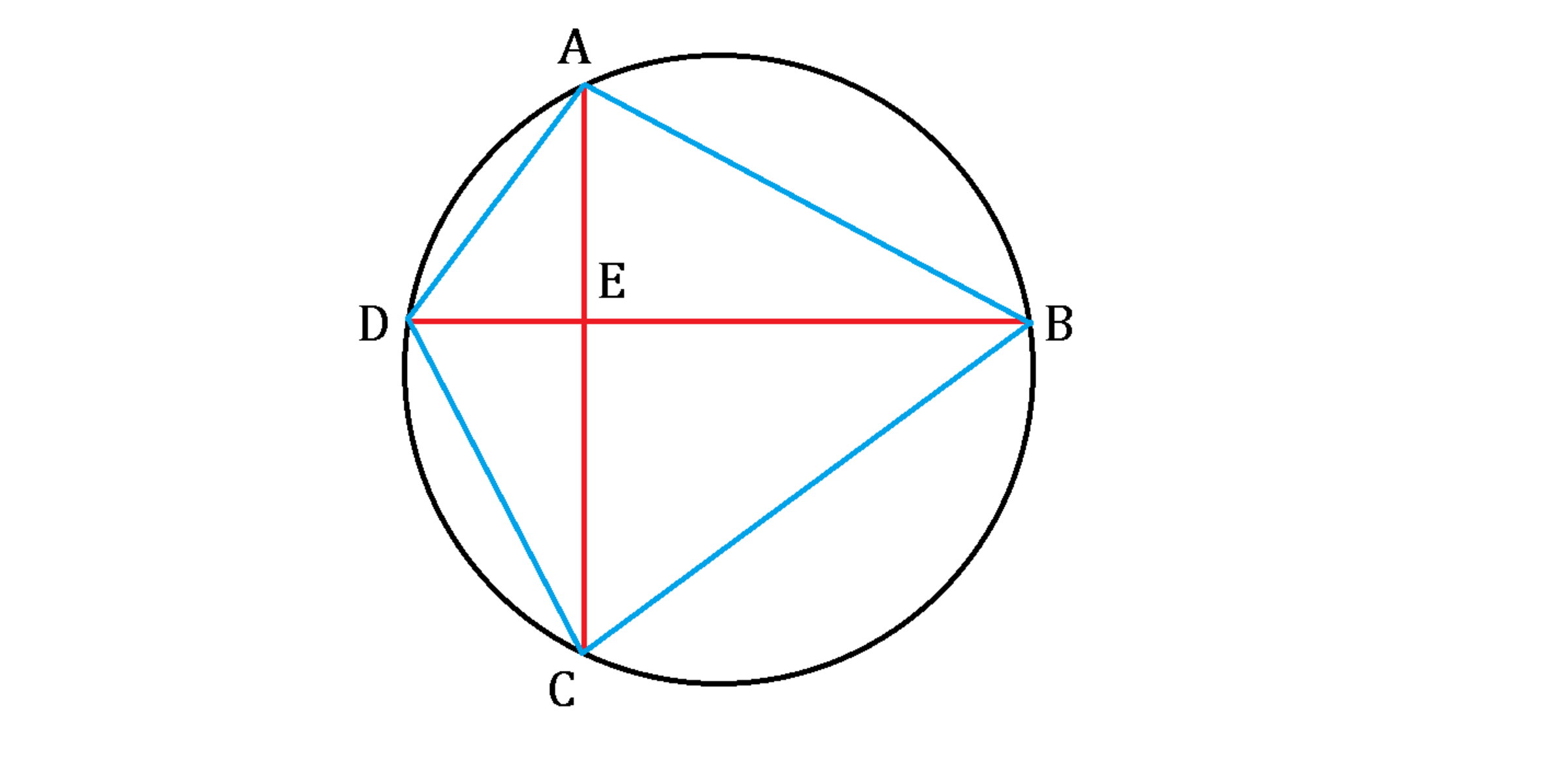
Once upon a time, Ptolemy drew 2 red perpendicular lines of length $AC = 56$ and $BD = 63$ and said, "This is a special intersection as the lengths from point $E$ to other vertices are all in integers."

Brahmagupta then drew 4 blue lines, connecting the vertices, and created a quadrilateral. "This is a unique quadrilateral," he claimed, "as the 4 side lengths are all in integers."

Finally, Parameshvara drew a circle, circumscribing that quadrilateral before declaring, "This is a wonderful circle, for its diameter also has the length in integer."

What is the length of this circumcircle's diameter according to these 3 wisemen?

The answer is 65.

1 solution

Worranat Pakornrat
Oct 5, 2016

Let $AE = a$ and $BE = b$ for some integers $a, b$ . Then $CE = 56 - a$ and $DE = 63 - b$ .

According to the chord theorem, $AE \cdot CE = BE \cdot DE$ .

Thus, $a(56 - a) = b(63 - b)$ __(1)

Then by Ptolemy's Theorem , $AC \cdot BD = AB \cdot CD + AD \cdot BC$

By Pythagorean Theorem, $AB = \sqrt{a^2 + b^2}$ , $BC = \sqrt{(56-a)^2 + b^2}$ , $CD = \sqrt{(56-a)^2 + (63-b)^2}$ , $DA = \sqrt{a^2 + (63-b)^2}$ .

Thus, $56 \cdot 63 = \sqrt{(a^2 + b^2)[(56-a)^2 + (63-b)^2]} + \sqrt{[(56-a)^2 + b^2][a^2 + (63-b)^2]}$ _(2)

Solving for the $2$ equations, we will obtain the side lengths of quadrilateral: $25, 39, 60, 52$ .

The area of the quadrilateral is $\dfrac{1}{2}(56\times63$ = 1764)

Then by using Parameshvara's formula, we can compute the radius of the circumcircle as:

$R = \dfrac{1}{4\times 1764}\sqrt{(25\times39 + 60\times 52) +(25\times 60 + 39\times 52) +(25\times 52 + 39\times 60)} = \dfrac{65}{2}$ .

Therefore, the diameter of the circumcircle equals $\boxed{65}$ .

How stupid of me: didnt look further for that formula so i ended up clicking discuss solution. I came to the integer lengtes so i actually was close. I worked from multiples of the 3-4-5 triangle to find them.

Peter van der Linden - 4 years, 8 months ago

The 3 Wisemen

The answer is 65.

1 solution

0 pending reports