The angle bisector
Δ A B C is a right triangle with B A C as the right angle and A B = 3 , A C = 6 . A D is the bisector of B A C . What is the length of A D ?
Give your answer rounded to the nearest hundredth.
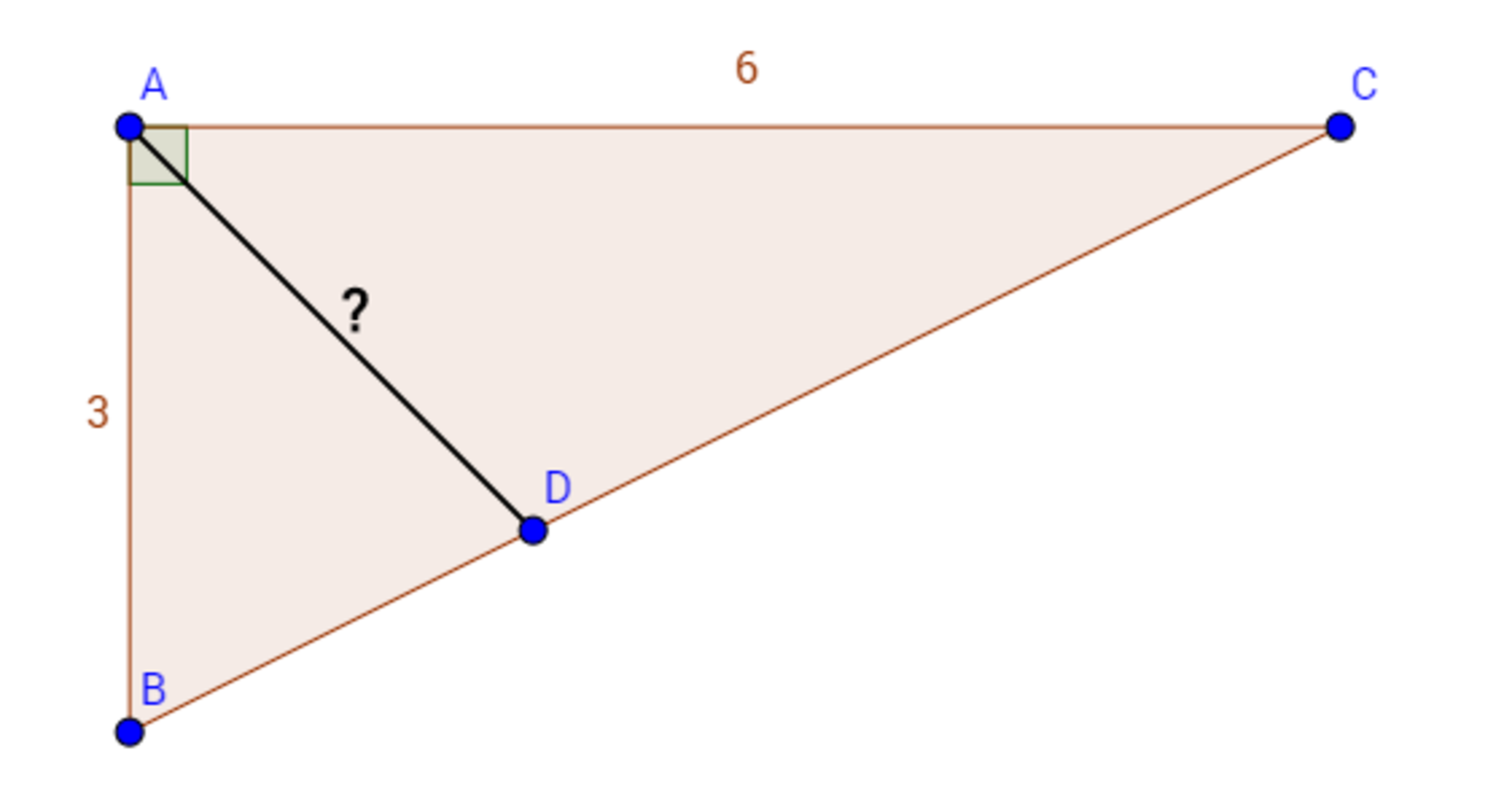
The answer is 2.83.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Great Solution!
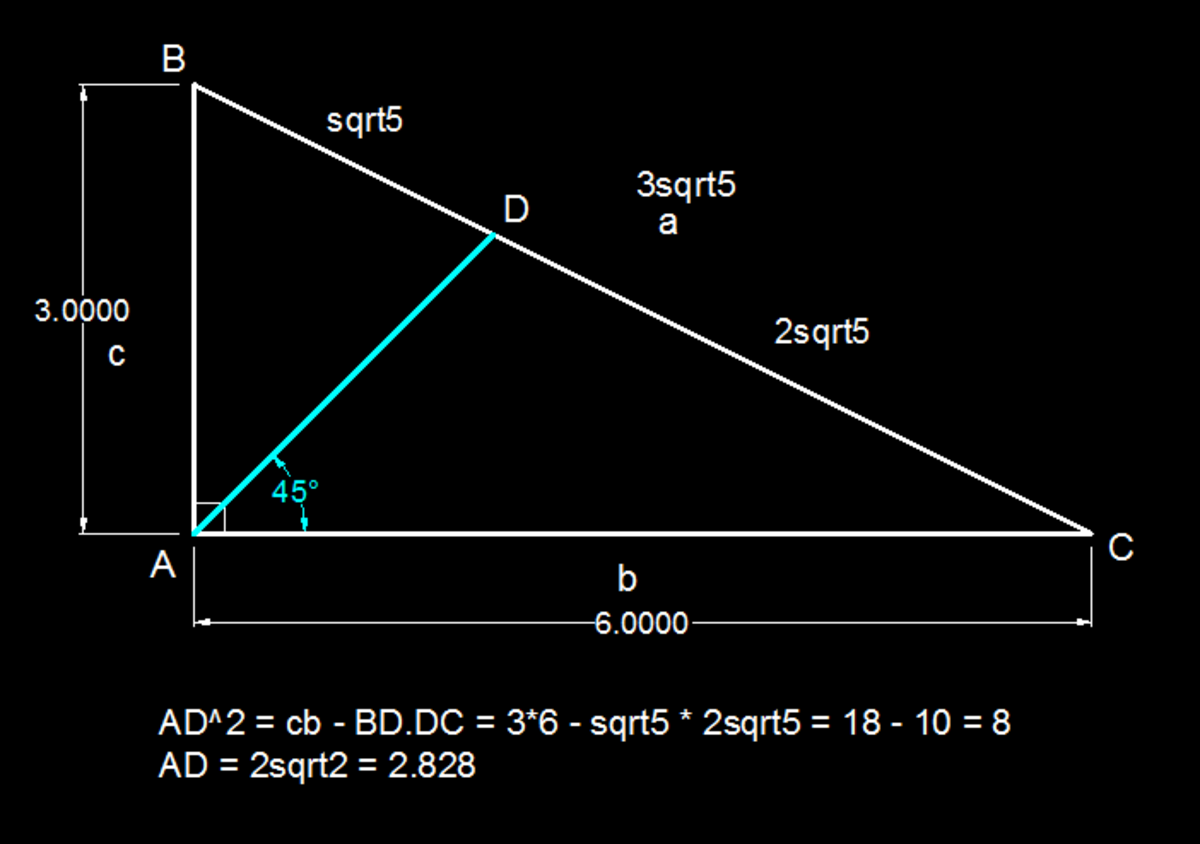
By the angle bisector theorem, we know that D C B D = 2 1 Therefore, we can let B D = x and D C = 2 x Then, we have the equation: 3 x = 4 5 ⇒ x = 5 By the cosine rule, 5 = 9 + A D 2 − 6 cos 4 5 ∘ A D Solving, AD = 2.83
Great solution 🙌
I think there are some few ways to solve this with only congruent triangles. Anyway, good, short, first solution :)
Inverse tan(6/3) = 63.43 degrees = angle B
Angle BAD = 1/2 of Angle BAC = 45 degrees
Angle ADB = 180 -45 - 63.43 = 71.57 degrees
Law of Sines : AD/sin 63.43 = 3/sin 71.57
AD = 2.83
I haven't learn the bisector theorem yet so I have another solution without using it.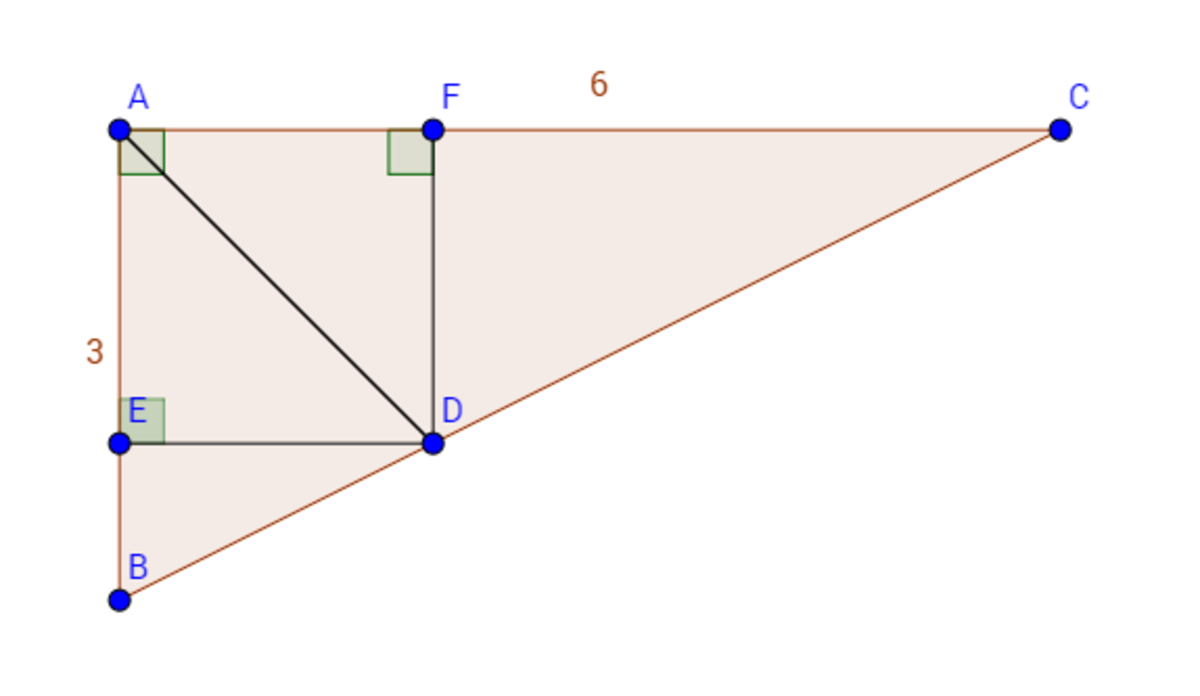 Because AD is the bisector of angle BAC, which is a right angle, so
B
A
D
=
C
A
D
=
4
5
∘
. Immediately, I think about isosceles right triangle. Thus I draw
D
E
⊥
A
B
and
D
F
⊥
A
C
. By SA for right triangles I got
△
A
E
D
≅
△
A
F
D
, so DE = DF. But DE and DF also the altitude of
△
A
D
B
and
△
A
D
C
, and I can find the area of
△
A
D
B
,
△
A
D
C
and
△
A
B
C
(let
[
△
A
B
C
]
be the area of triangle ABC):
[
△
A
B
D
]
=
2
A
B
⋅
D
E
=
2
3
D
E
[
△
A
C
D
]
=
2
A
C
⋅
D
F
=
3
D
E
[
△
A
B
C
]
=
2
A
B
⋅
A
C
=
9
[
△
A
B
D
]
+
[
△
A
C
D
]
=
[
△
A
B
C
]
Hence:
2
3
D
E
+
3
D
E
=
9
⇒
D
E
=
2
Proving that ADE is an isosceles right triangle is easy and thanks to Pythagorean theorem, we are done:
A
D
=
D
E
2
+
D
E
2
=
2
2
≈
2
.
8
3
. Also, you can draw altitudes from B and C, then use area of triangles, too (and sorry for my bad English, I am not good at English)
Because AD is the bisector of angle BAC, which is a right angle, so
B
A
D
=
C
A
D
=
4
5
∘
. Immediately, I think about isosceles right triangle. Thus I draw
D
E
⊥
A
B
and
D
F
⊥
A
C
. By SA for right triangles I got
△
A
E
D
≅
△
A
F
D
, so DE = DF. But DE and DF also the altitude of
△
A
D
B
and
△
A
D
C
, and I can find the area of
△
A
D
B
,
△
A
D
C
and
△
A
B
C
(let
[
△
A
B
C
]
be the area of triangle ABC):
[
△
A
B
D
]
=
2
A
B
⋅
D
E
=
2
3
D
E
[
△
A
C
D
]
=
2
A
C
⋅
D
F
=
3
D
E
[
△
A
B
C
]
=
2
A
B
⋅
A
C
=
9
[
△
A
B
D
]
+
[
△
A
C
D
]
=
[
△
A
B
C
]
Hence:
2
3
D
E
+
3
D
E
=
9
⇒
D
E
=
2
Proving that ADE is an isosceles right triangle is easy and thanks to Pythagorean theorem, we are done:
A
D
=
D
E
2
+
D
E
2
=
2
2
≈
2
.
8
3
. Also, you can draw altitudes from B and C, then use area of triangles, too (and sorry for my bad English, I am not good at English)