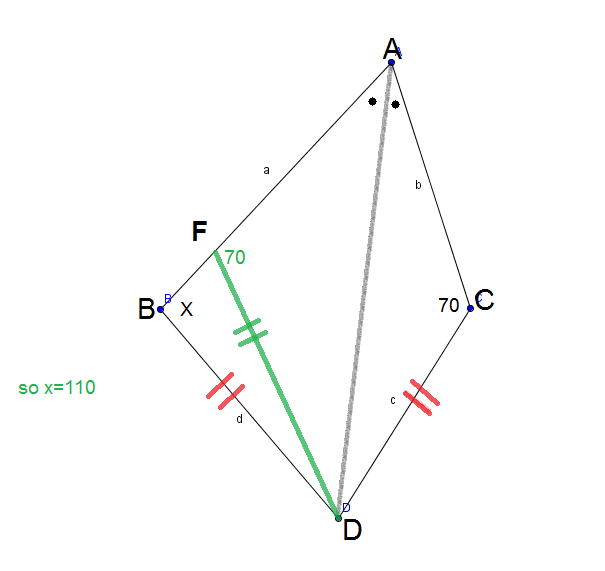
The Angle problem
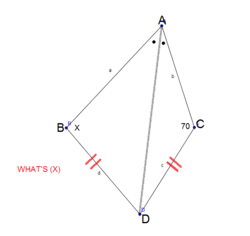 We are given that
∠
B
A
D
=
∠
D
A
C
,
B
D
=
D
C
,
A
B
=
A
C
and
∠
A
C
D
=
7
0
∘
.
We are given that
∠
B
A
D
=
∠
D
A
C
,
B
D
=
D
C
,
A
B
=
A
C
and
∠
A
C
D
=
7
0
∘
.
What is the value of x ?
Note the diagram is not to scale.
The answer is 110.000.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
The quadrilateral is cyclic by definition. Hence answer is 180°-70°=110°.
What definition statetd that this paticular quadrilateral is cyclic?
how it is cyclic quadrilateral pls explain ??
Log in to reply
Hi... I know it may be late... but still here is why the quadrilateral is cyclic. I'll take trigonometric approach.
First off let's split the quadrilateral into triangles △ A B D and △ A C D .
Applying sine rule on both triangles, we observe that sin ∠ B A D ∣ B D ∣ = sin ∠ A B D ∣ A D ∣ and sin ∠ C A D ∣ D C ∣ = sin ∠ A C D ∣ A D ∣ . However since ∠ B A D = ∠ C A D and ∣ B D ∣ = ∣ C D ∣ , we can conclude that sin ∠ A B D ∣ A D ∣ = sin ∠ A C D ∣ A D ∣ .
Now we see that the two triangles △ A B D and △ A C D are never congruent as two of their side lengths are the same and ∣ A B ∣ = ∣ A C ∣ . Also ∠ B A D = ∠ C A D which means that there are no more equal angles in these two triangles, as if one pair of the angles are equal, the other angle pair will be equal also and the triangles will be congruent by AAS.
What this means is that relating back to sin ∠ A B D ∣ A D ∣ = sin ∠ A C D ∣ A D ∣ , we also know that sin θ = sin ( 1 8 0 o − θ ) . So ∠ A B D + ∠ A C D = ∠ A B D + ( 1 8 0 o − ∠ A B D ) = 1 8 0 o , hence the quadrilateral is cyclic as opposite angles add up to 1 8 0 o .
When nothing click use cosine formula ..and ans comes in 3 line work
The green line is on the wrong side of BD although it won't change the answer.
Log in to reply
Ya . I made that wrongly I will correct it
could you please explain the answer?
Log in to reply
we can make the green line to make DFA Identical to ACD
if BD=DF , mDBF=mBFD=110 ,Which is impossible ,am i right .Could you explain
The correct diagram for the solution should reflect the fact that
7
0
∘
is an acute angle.
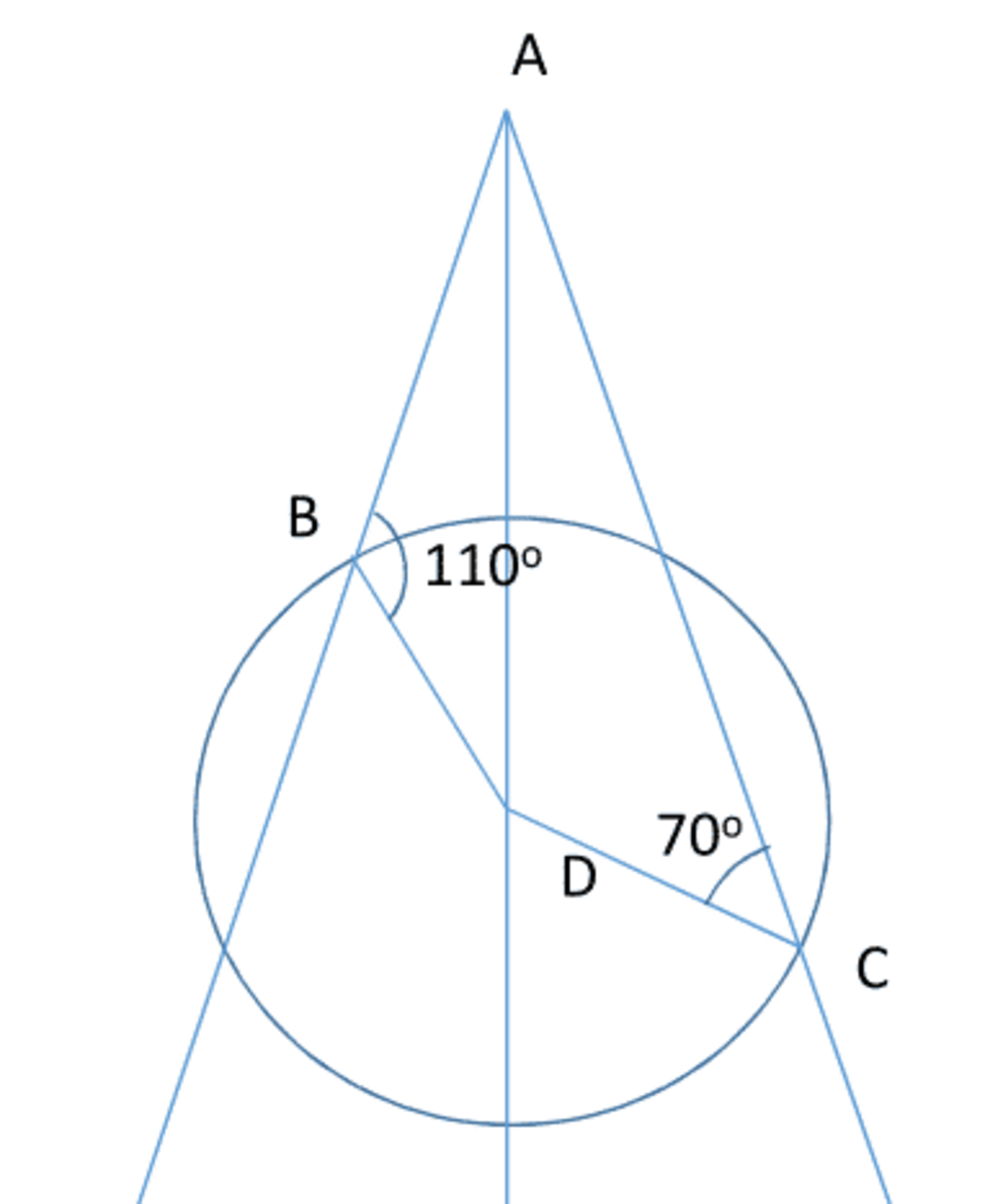
It is cyclic because if we consider the point that the angle bisector intersects on the circumcircle, it should be equidistant from the two vertices because the arcs are equal. Converse is true.
 Two possible triangles
Two possible triangles
This is a beautiful example of why we do not have a ASS (Angle Side Side) test of congruence. Using such data for constructing a triangle yields two alternate triangles, given in the statement as △ A C D and △ A B D as follows -
-
Draw base AD
-
Draw locus of point C (direction of line AC) at given \(angle DAC)
3. Cut line [2] with an arc of radius DC and center D, to get the two possible positions (C1 and C2) of point C Giving triangles \( \triangle ADC1 \) and △ A D C 2
In △ C 1 C 2 D DC1 = DC2 so ∠ D C 1 C 2 = ∠ D C 2 C 1 = 7 0 ° Hence ∠ D C 1 A = x = 1 1 0 °
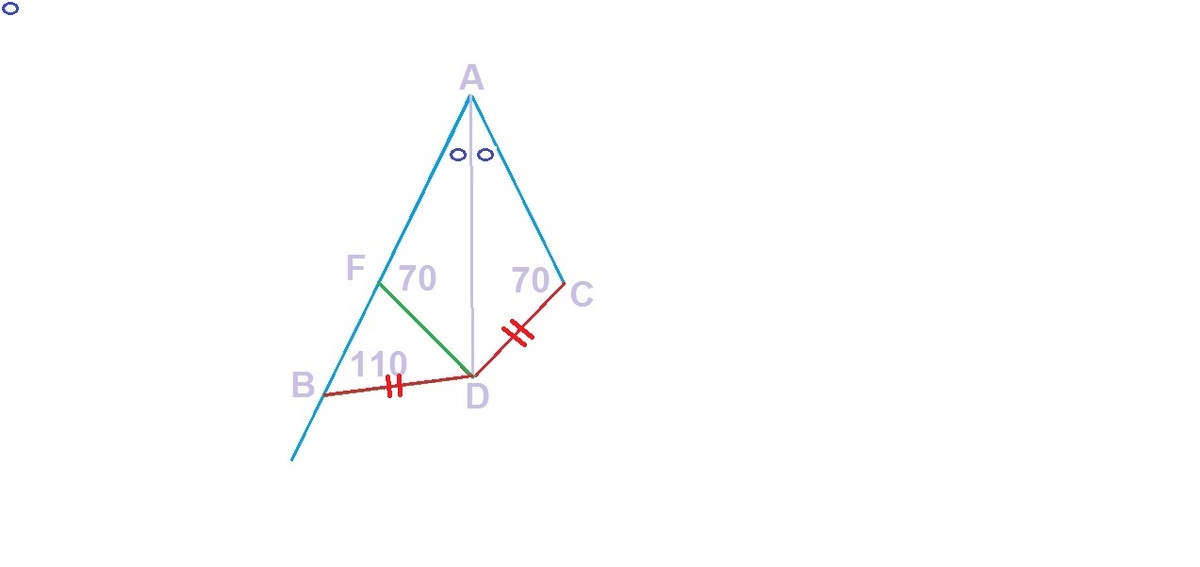 Diagram explains the solution.
Diagram explains the solution.