The Angly kid :0

Geometry Level 2

Adrian went to get his face pierced .He was having a great day until the piecer asked him a weird question (that made him angry) and told him that he will only continue after getting a correct answer.

Angly Adrian Angly Adrian

The question is as follows :

What is the sum of all the angles of your face?? ( marked ones ) \textcolor{#D61F06}{\text{What is the sum of all the angles of your face??}}\tiny{(\text{marked ones})}

Adrian is an emo and not so good at math .Being his frmd and good at math ,can you help him find the correct answer?

∞ ∞ 360° 1080° 1800° 720° 1440°

Agent T by Agent T , 17, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

3 solutions

Agent T
May 16, 2021

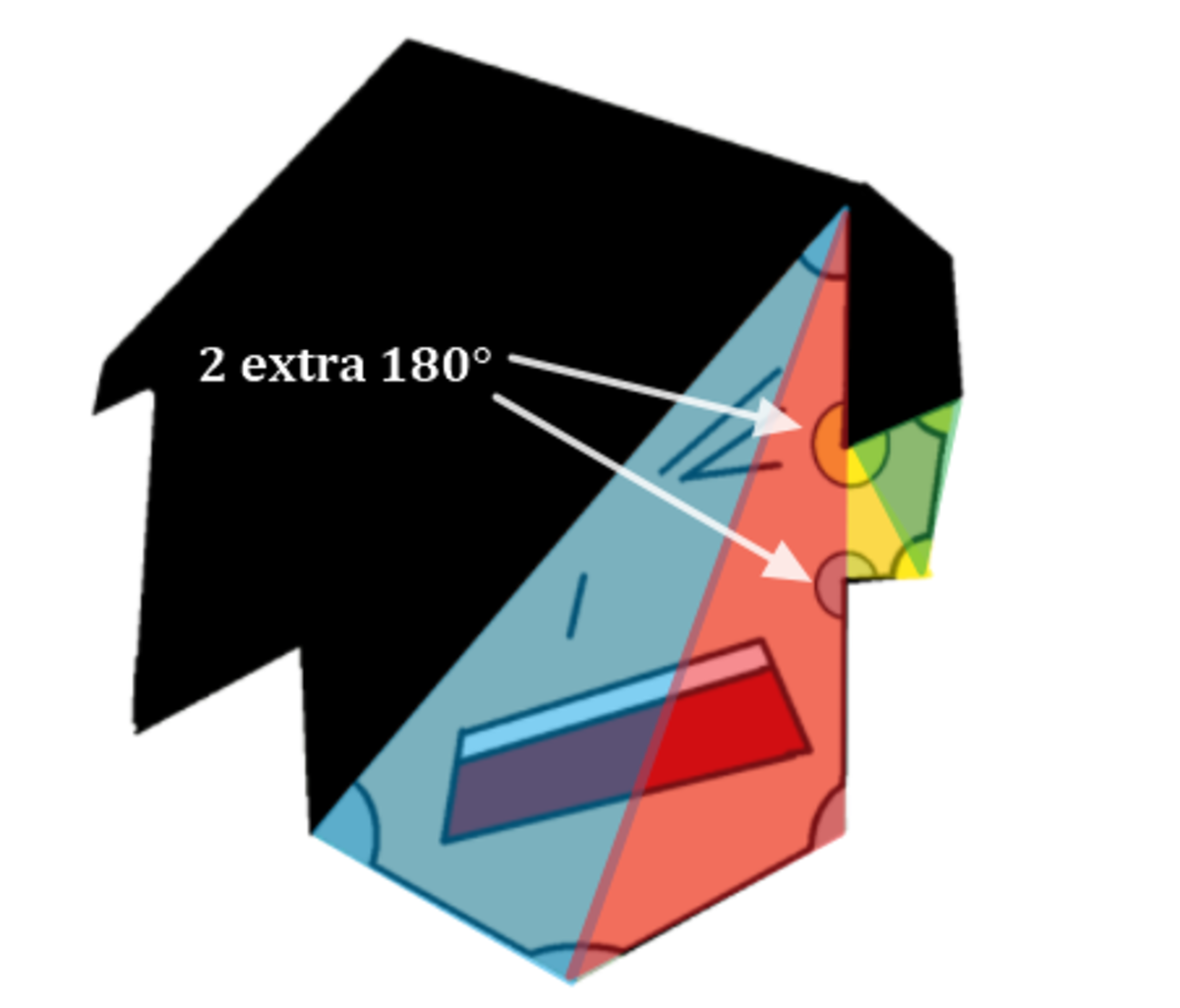
The sum of interior angles of a n-gon is given by the formula:

n ∗ 180 = 360 − s u m \textcolor{#D61F06}{\boxed{\textcolor{#3D99F6}{n*180=360-sum}}}

There are 8 sides in this case ,so

8 ∗ 180 − 360 = s u m 8*180-360=sum

4 ∗ 360 − 360 = s u m 4*360-360=sum

360 ( 4 − 1 ) = s u m 360(4-1)=sum

360 ∗ 3 = s u m 360*3=sum

= > s u m = 1080 ° =>sum=1080°

Boom!

4 Helpful 2 Interesting 3 Brilliant 0 Confused
Ill Banin
Jun 1, 2021

Octagonal is 135×8 = 1080°, so answer is 1080°.

1 Helpful 1 Interesting 1 Brilliant 0 Confused

Noice work!!

Agent T - 1 week, 4 days ago
David Stiff
May 20, 2021

The sum of the angles in a triangle is 180 ° 180\degree . We can break up his face into four triangles. However, there are two extra 180 ° 180\degree angles to account for (labelled in the picture). Thus the sum of the angles is 6 × 180 ° = 1080 ° 6 \times 180\degree = \boxed{1080\degree}

1 Helpful 1 Interesting 1 Brilliant 0 Confused

You actually derived the formula for an eight sided polygon !! Great work!!

Agent T - 3 weeks, 1 day ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...