The angular traversing

Geometry Level 3

There are two circles. One with centre A [say circle A] whose radius is fixed and cannot be changed and one with center C [say circle C] whose radius can be varied with the help of a point B which lies on the circumference of the circle with center A.

Right now both the circles viz. Circle A and Circle B have equal radii(As shown). The point B is right now in its $initial$ position.

Now, it traversed on the radius of the Circle A and reached a point where the point A, B and C are collinear(as shown below). Assume angle CAB=180°. Let's call this position of point B as $final$ position.

What angle is subtended to the center of the Circle A by the arc which is being traversed by point B from its $initial$ to $final$ position?

NOTE : The point B is bound to traverse on the circumference of the Circle A. And the point C is fixed and cannot move.

The figures drawn are just to give an idea of the question.The assumptions are to be taken, as the answer is with respect to the assumption.

90 135 180 120 150

1 solution

Abhay Tiwari
Apr 21, 2016

Initial position: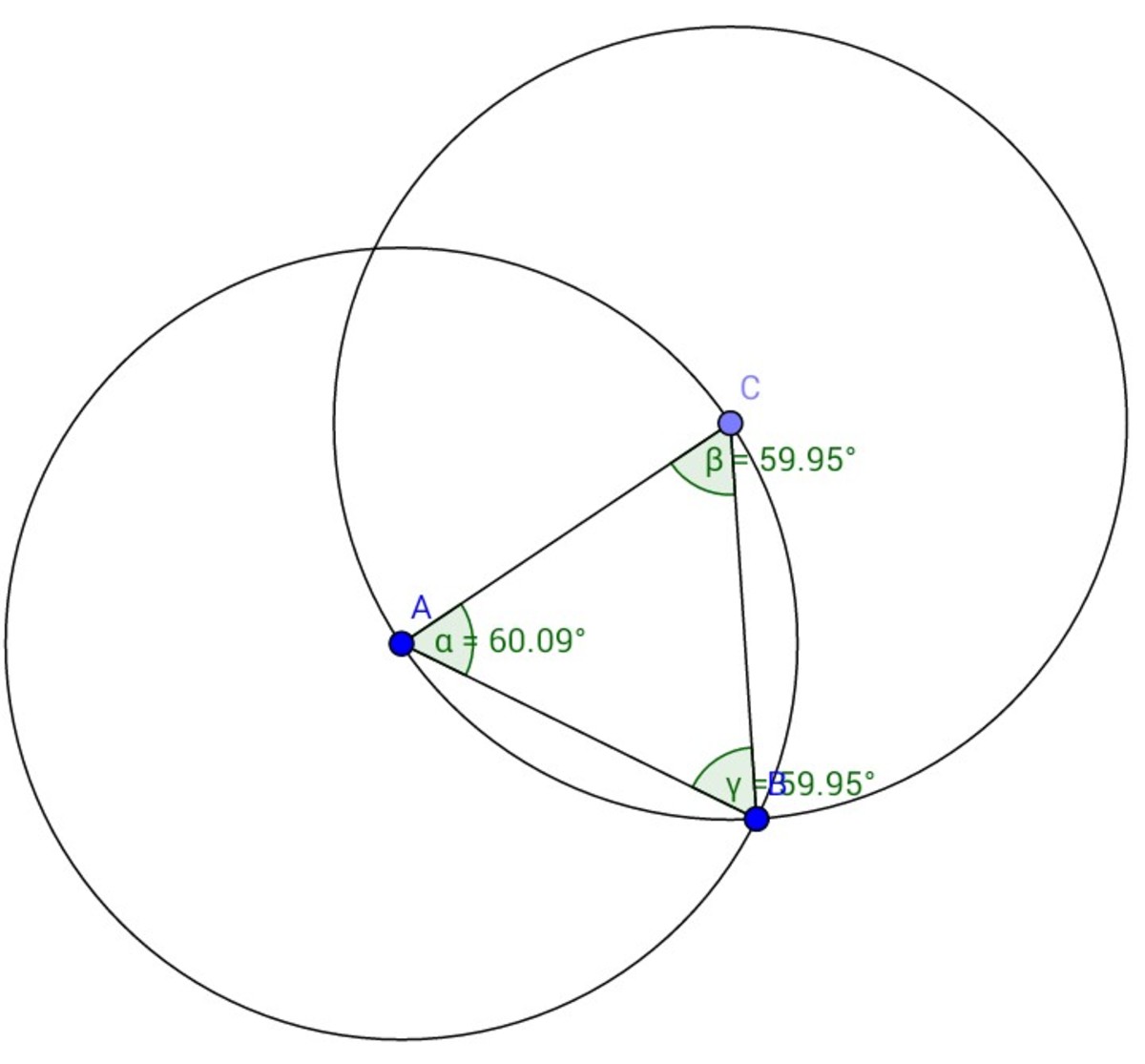

The two circles have equal radii therefore at this initial position side AB=BC=CA, forming an equilateral triangle. Each angle is 60°.

Angle $CAB_{initial}=60°$ (don't go with the figure, it is just for an idea)

Final position::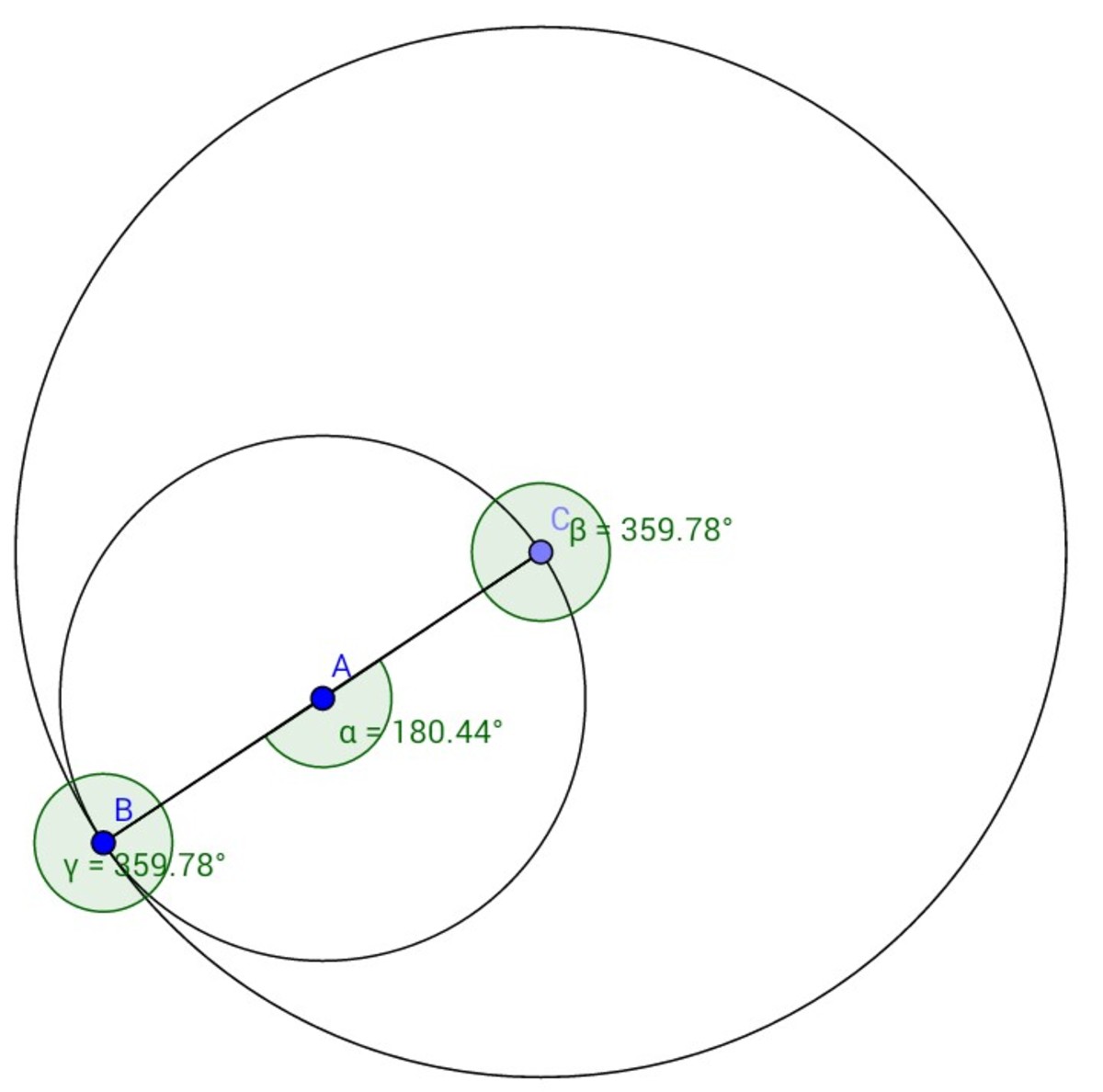

For final position, all the points are collinear.

Angle $CAB_{final}=180°$

Angle subtended by the Angle being traversed by point B from initial to final position= Difference between the two angles:

$CAB_{final}-CAB_{initial}=180°-60°=\boxed{120°}$

The angular traversing

1 solution

0 pending reports