A classical mechanics problem by Tanay Kibe

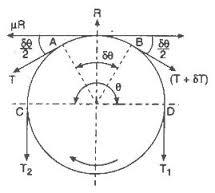Consider a pulley as shown. A string is placed on the pulley. The string is massless and the pulley has friction. Consider the two tensions $T_1$ and $T_2$ , with $T_1>T_2$ .

The coefficient of friction is $k$ . Find the ratio $\dfrac{ T_1}{T_2}$ when the string is just about to slip over the pulley.

Details and Assumptions:

• Take $k =\frac1\pi , \theta = \pi$ .

• Use the approximation $e = 2.71$ .