The answer is n 2
2 − α 1 3 1 + 2 − α 2 3 1 + 2 − α 3 3 1 + 2 − α 4 3 1
Given that 1 , α 1 , α 2 , α 3 , α 4 are distinct fifth roots of unity, evaluate the expression above.
The answer is 49.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
10 solutions
Great way for those who are familiar with manipulating with calculus.
There is another more intuitive approach, which looks at finding the polynomial whose roots are 2 − α i . Can anyone add that as a solution?
If instead of 2 - a_(i), we have 1 - a(i) Then
nice solution dude.
WTF this is awesome! Would've never thought of it this way! :D (Even though there is a step which involves calculus, which I've completely forgotten...) MASSIVE UPVOTE!
Great solution dude.. Awsome I loved it.
So, the value of n is 7..because ''the answer is n squared''! (just joking!)
if a 1 , a 2 , . . . . . a n are the roots of f ( x ) = 0 , then f ( x ) f ′ ( x ) = i = 1 ∑ n x − a i 1 .
Considering f ( x ) = x 5 − 1 here and using the above property, we have
x 5 − 1 5 x 4 = x − 1 1 + x − α 1 1 + x − α 2 1 + x − α 3 1 + x − α 4 1 .
Putting x = 2 we get
3 1 8 0 = 1 1 + 2 − α 1 1 + 2 − α 2 1 + 2 − α 3 1 + 2 − α 4 1
⟹ 2 − α 1 3 1 + 2 − α 2 3 1 + 2 − α 3 3 1 + 2 − α 4 3 1 = 4 9 .
Interesting! I never knew this property of polynomials
Can you prove that the property of the polynomials always holds Sandeep?
Log in to reply
Since over complex numbers, a equation of degree n always has n roots, it can be written as f ( x ) = i = 1 ∏ n ( x − a i )
Differenciating using the product rule, we find that the differenciated result is a sum of many terms where in each term, one of the ( x − a i ) is missing. f ′ ( x ) = ( x − a 2 ) ( x − a 3 ) ( x − a 4 ) … ( x − a n ) + ( x − a 1 ) ( x − a 3 ) ( x − a 4 ) … ( x − a n ) + ( x − a 1 ) ( x − a 2 ) ( x − a 4 ) … ( x − a n ) + ⋯ + ( x − a 1 ) ( x − a 2 ) ( x − a 3 ) … ( x − a n − 1 ) = i = 1 ∑ n x − a i f ( x ) Hence the result follows. (It also holds when the leading coefficient isn't 1)
@Sandeep Bhardwaj Best solution
Calculus method is best & easiest but i am posting a different method.
1 + x + x 2 + x 3 + x 4 = ( x − α 1 ) ( x − α 2 ) ( x − α 3 ) ( x − α 4 ) L e t x = 2 − t & 2 − α = β P = 1 + ( 2 − t ) + ( 2 − t ) 2 + ( 2 − t ) 3 + ( 2 − t ) 4 & ( 2 − t − α 1 ) ( 2 − t − α 2 ) ( 2 − t − α 3 ) ( 2 − t − α 4 ) = ( t − β 1 ) ( t − β 2 ) ( t − β 3 ) ( t − β 4 ) ∴ P = ( t − β 1 ) ( t − β 2 ) ( t − β 3 ) ( t − β 4 ) ∴ β 1 1 + β 2 1 + β 3 1 + β 4 1 = β 1 β 2 β 3 β 4 ∑ β 1 β 2 β 3 = c o n s t . t e r m i n P − c o f f . o f t i n P = ( − 1 ) 1 + 2 + 2 2 + 2 3 + 2 4 { − 1 − 2 1 ( 2 1 ) − 2 2 ( 3 1 ) − 2 3 ( 4 1 ) } = 3 1 4 9 ∴ 2 − α 1 3 1 + 2 − α 2 3 1 + 2 − α 3 3 1 + 2 − α 4 3 1 = 4 9
The required expression can be rewritten as i = 1 ∑ 4 2 − α i 2 5 − α i 5 .
We see that x − a x 5 − a 5 = x 4 + a x 3 + a 2 x 2 + a 3 x + a 4 . After substituting x = 2 and a = α i , the required expression becomes i = 1 ∑ 4 ( 1 6 + 8 α i + 4 α i 2 + 2 α i 3 + α i 4 )
Since i = 1 ∑ 4 α i = i = 1 ∑ 4 α i 2 = i = 1 ∑ 4 α i 3 = i = 1 ∑ 4 α i 4 = − 1 , the expression becomes 1 6 × 4 + ( − 1 ) ( 8 + 4 + 2 + 1 ) = 6 4 − 1 5 = 4 9
superb solution!! :D really ingenious !
Log in to reply
Thanks :) I noticed that no one else had used the fact that 3 1 = 2 5 − 1 , so I posted this solution.
Elegant solution. Relatively, I spent too much time on a brutal way. XD
I have solved this by calculus, but instead i will be posting a different solution.
Since α 1 , α 2 , α 3 , α 4 are four of the five 5 t h roots of unity, we have:
P ( x ) = x 4 + x 3 + x 2 + x + 1 which have the roots: α 1 , α 2 , α 3 , α 4
Note that we need to find 3 1 . ∑ 2 − x k 1 where x k are the roots of P ( x ) .
Let: y k = 2 − x k 1 so, we need to find ∑ y k
A short computation yields x k = y k 2 y k − 1
Plugging this in P ( x ) , we get:
( y k 2 y k − 1 ) 4 + ( y k 2 y k − 1 ) 3 + ( y k 2 y k − 1 ) 2 + y k 2 y k − 1 + 1 = 0
Multiplying by y k 4 , we get
y k 4 + y k 3 ( 2 y k − 1 ) + y k 2 ( 2 y k − 1 ) 2 + y k ( 2 y k − 1 ) 3 + ( 2 y k − 1 ) 4
It is easy to observe that :
coefficeint of y k 4 = 1 + 2 + 2 2 + 2 3 + 2 4 = 3 1
coefficeint of y k 3 = − ( 1 + 2 . 2 C 1 + 2 2 . 3 C 2 + 2 3 . 4 C 3 ) = − 4 9
∴ ∑ y k = − 3 1 − 4 9 = 3 1 4 9
⟹ 3 1 . ∑ 2 − x k 1 = 3 1 . ∑ y k = 4 9
@Calvin Lin . i think you were thinking of something like this? :D
That's one way to get the polynomial, via a change of variables, so that the roots are y = 2 − x 1 .
I also like Ayush's approach above, where he made the roots β = 2 − α , and then proceeded to find ∑ β 1 .
Log in to reply
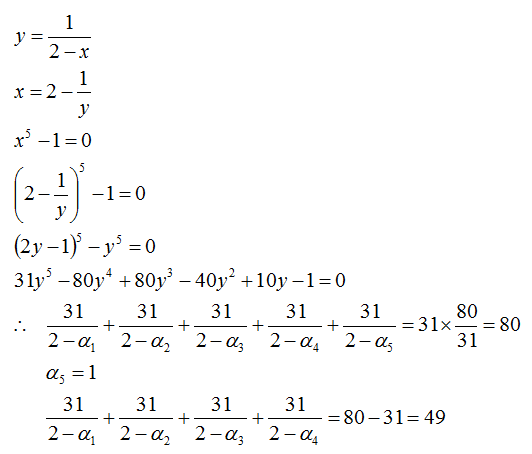
yes, it was a good solution
First of all, this method is long and not advisable too but just I am sharing for clarity.
Well, we can see that 5th root of unity means α 5 = 1
α 5 = e 2 n ι π
α = e 5 2 n ι π
So, α 1 = e 5 2 ι π
α 2 = e 5 4 ι π
α 3 = e 5 6 ι π
α 4 = e 5 8 ι π
α 5 = e 5 1 0 ι π = e 2 ι π = 1
And similarly, α 6 = e 5 1 2 ι π , but wait,
e 5 1 2 ι π = e 2 ι π + 5 2 ι π = e 5 2 ι π
So, we got our 4 5 t h roots of unity. Hence, substituting,
3 1 ( 2 − e 5 2 ι π 1 + 2 − e 5 4 ι π 1 + 2 − e 5 6 ι π 1 + 2 − e 5 8 ι π 1 )
We know that e ι x = c o s x + ι s i n x
Now, using some trigonometry, we can further simplify it as -
3 1 ( 1 + 2 5 − 2 0 ( c o s 5 4 π + c o s 5 2 π ) + 1 6 c o s 5 2 π c o s 5 4 π 1 5 − 6 ( c o s 5 4 π + c o s 5 2 π )
We know that -
c o s 5 4 π + c o s 5 2 π = − 2 1
c o s 5 2 π c o s 5 4 π = − 4 1
Substituting both these in the above equation -
3 1 ( 1 + 3 1 1 8 ) = 4 9
I hope this method to be the easiest..
The question involves Complex Numbers. Then, why can't we use complex guys?
Notice one thing
Let a general solution of the roots be α
Fifth root of unity then can be
G i v e n R e n a m e 1 1 α 1 α α 2 α 2 α 3 α 3 α 4 α 4
And they're cyclic (or whatever term it is called)
Also notice
i = 1 ∑ 4 α i = ∑ α = ∑ α 2 = ∑ α 3 = ∑ α 4
Now begins the FIGHT
3 1 = 2 5 − α 5 ⇒ 2 − α 3 1 = 2 − α 2 5 − α 5 = 2 4 + 2 3 α + 2 2 α 2 + 2 α 3 + α 4
⇒ 1 ∑ 4 2 − α 2 5 − α 5 = 4 ⋅ 2 4 + 2 3 ( ∑ α ) + 2 2 ( ∑ α 2 ) \nonumber + 2 ( ∑ α 3 ) + ( ∑ α 4 )
To get ∑ α , take the equation
x 5 = 1 OR x 5 − 1 = 0
⇒ 1 + ∑ α ⇒ ∑ α ⇒ ∑ α = 0 = − 1 = ∑ α 2 = ∑ α 3 = ∑ α 4 = − 1
Hence the answer,
⇒ 1 ∑ 4 2 − α 2 5 − α 5 = 4 ⋅ 2 4 − 2 3 − 2 2 − 2 − 1 = 6 4 − 8 − 4 − 2 − 1 = 4 9
∴ Answer is 4 9
Moderator note:
It is typically hard to really demonstrate that a particular method is the easiest.
For example, my approach would be to create a polynomial whose roots are 2 − α i 1 , and then apply Veita's to find the sum of roots. That, to me, is much easier, especially once you understand how to extend this concept to other such similar cases.
In other cases, if the number of number of roots of unity given is odd, you can use this method.
How is sigma alpha = sigma (alpha)^2 and so on. I couldn't understand that part.
Thanks for the nice question.

Moderator note:
The approach that you took is somewhat long-winded, and could be simplified greatly. The idea is indeed to find a polynomial whose roots are ( 2 − α i ) .
Note: Can you clarify the last line? I'm not sure how you obtained 49 from it.
We need to calculate sum of roots of g(x) taken three at a time because when I have added 1,2,3,4 see what I got as E. By vieta's relation this is equal to -(coeff ofx)/coeff of x^3 It may be long winded but I will say this approach is unique and different from what others have posted here so that we get a new solution.
Let n = 2 − a 3 1
Some algebra yields a n = 2 n − 3 1
Raising both sides of this equation by 5, we get
n 5 = 3 2 n 5 − 5 ∗ 2 4 3 1 n 4 + . . .
By Vieta's , the sum of the five values of n is 3 1 5 ∗ 2 4 ∗ 3 1 = 8 0
But why are there five values of n when there are only four terms in our problem? This is because we included the non-existent term n = 2 − 1 3 1 = 3 1 when we raised the equation to the 5th power.
Thus, the sum of the four terms in the problem is
8 0 − 3 1 = 4 9
Nice but why is the sum of values divided by 31 and not 32 when sum of the values is -b/a??
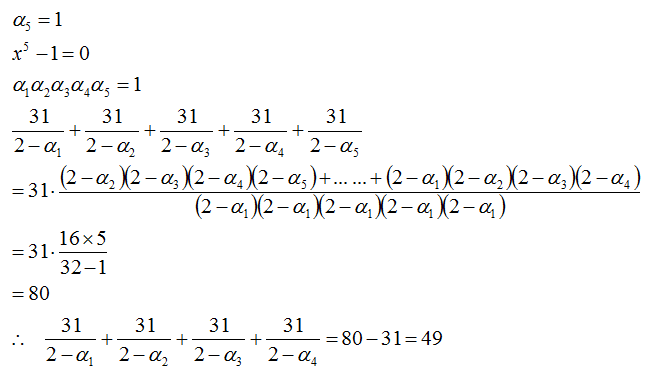
As 1 , α 1 , ⋯ , α 4 are roots of the equation x 5 − 1 = 0 , ( x − 1 ) i = 1 ∏ 4 ( x − α i ) i = 1 ∏ 4 ( x − α i ) = x 5 − 1 = x − 1 x 5 − 1
Take the natural logarithm on both the sides and then differentiate wrt x .
i = 1 ∑ 4 lo g ( x − α i ) i = 1 ∑ 4 x − α i 1 = lo g ( x 5 − 1 ) − lo g ( x − 1 ) = x 5 − 1 5 x 4 − x − 1 1 Substitute x = 2 in the above obtained equality to see that i = 1 ∑ 4 2 − α i 1 = 3 1 4 9 ∴ i = 1 ∑ 4 2 − α i 3 1 = 4 9