The Answer Is Quite Large
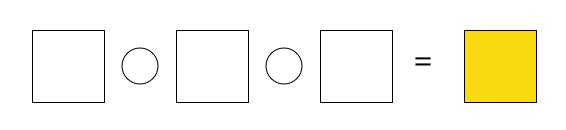
On the left side of the above equation, fill in each square with a distinct digit (0 to 9), and each circle with one of the 4 arithmetic operations ( + , − , × , ÷ ) with repeated use allowed.
Then we can generate a sequence of positive integers (with common difference 1) on the right side as follows (or in various other ways): 1 × 3 − 2 5 − 3 × 1 1 + 4 − 2 8 ÷ 2 ÷ 1 = 1 = 2 = 3 = 4 ⋮ , where each result is obviously 1 more than the previous result.
But this can continue only up to a certain point. What is the first (least) positive integer for which this process fails to work?
Clarification: If you could generate the sequence only up to 120, your answer would be 121.
The answer is 81.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
How about 4 + 5 x 9
consider the forms
9 n − m , 9 n + m where m,n represent distinct digits
The interval 9 n + m and 9 ( n + 1 ) − p overlap
if n = m = x and ( n + 1 ) = p = y
for equality we have 9 x + x = 9 y − y
⇒ 1 0 x = 8 y or
( x , y ) = ( 4 , 5 )
we can see that all numbers from 1 to 7 9 except 4 0 can be represented using one of these forms
but , 4 0 = 8 × 5 + 0
Also note that 7 9 is the largest number that can be written in the form a × b + c
thus any larger number has to be of the form a × b × c
checking for 8 0 , we get 8 0 = 2 × 5 × 8
now 8 1 = 3 4 thus we get ,
3 a × 3 b × 3 c = 3 4
⇒ 3 a + b + c = 3 4 or
a + b + c = 4
now a,b,c needs to be distinct and 0 ≤ a , b , c ≤ 2
thus we find that a , b , c must be a permutation of ( 0 , 1 , 2 )
but,
0 + 1 + 2 = 3 = 4
thus the number 81 is impossible to represent .
Great ideas presented.
The "easily see that all number can be represented" should be explained with some substantiation. I'm often wary when I see the word "easily" or "obvious", and would think about why that's the case. In this scenario, as it turns out, 4 0 = 9 × 4 + 4 = 9 × 5 − 5 cannot be represented in the distinct digit form. How do we know that we've not missed other cases?
Log in to reply
Oops missed 40 hmm gotta edit it now , i was going for overlapping intervals from multiples of 9,
Now that i think about it 40 is the only exception.
The interval 9 n + m and 9 ( n + 1 ) − p overlap
if n = m = x and ( n + 1 ) = p = y
for equality we have,
9 x + x = 9 y − y
⇒ 1 0 x = 8 y or
( x , y ) = ( 4 , 5 )
will add this to the proof as well.
thanks for pointing out the error :)
Note that for 0 ≤ a , b ≤ 8 , 9 × a + b represents all integers between 0 and 80 inclusive. So if a = b , we can use this representation to give the number.
When a = b , the integer is 1 0 a = a × 5 × 2 , thus if a = 2 , 5 , we can use this representation to give the number.
When a = 2 , the number is 2 0 = 5 × 4 + 0 . When a = 5 , the number is 5 0 = 8 × 7 − 6 . Thus in fact, all positive integers not greater than 80 can be represented in this way.
For 81, suppose not all circles are multiplication signs. We claim its value can't be greater than 80. One way to do this is with case by case analysis (there are only 15 cases; most of them involve " a − b ≤ a " and " a ÷ b ≤ a ", and the rest uses a × b ≤ 7 2 only reachable when { a , b } = { 8 , 9 } , and a × b ≤ 6 3 otherwise). Thus we have a × b × c = 8 1 . Thus a , b , c must be perfect powers of 3, and thus must be 1 , 3 , 9 in some order. But then 1 × 3 × 9 = 2 7 = 8 1 , contradiction. So 81 is the smallest positive integer that cannot be represented in such way.