The ant goes marching
An ant is marching up a flat plane when it comes across something unexpected: a circular disc in the plane is inexplicably rotating clockwise.
It is directly in the way. The ant's path is a diameter of the circle. "No matter," thinks the ant, as it marches along its intended path. Only... after one minute the ant finds it has crossed the disc only to end up exactly where it started?
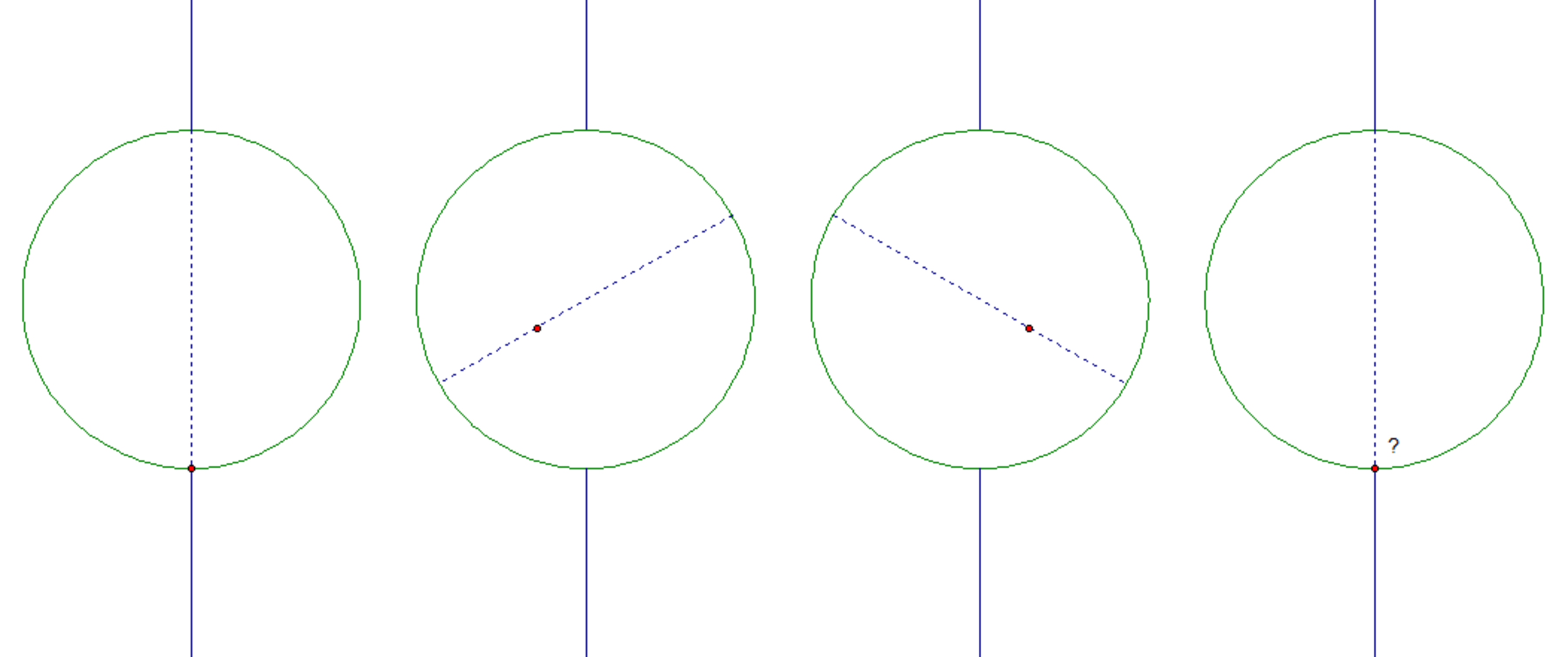
This ant is not going to be fooled twice. It chooses a chord, plots a course along it, and this time it steps off precisely where it means to. On the other side!
Question: How many seconds does it take the ant to get to the other side? Round to the nearest second.
Bonus: Is there a different path that would be quicker?
The answer is 36.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
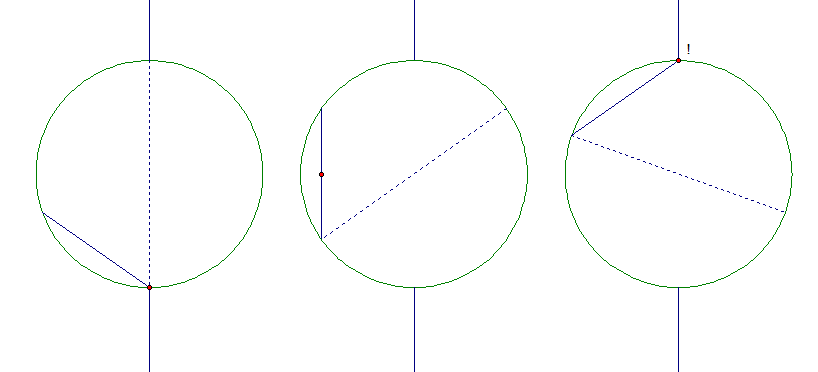
From the first attempted crossing, we know the disc rotates at . 5 r p m = m i n u t e 1 8 0 ∘ = s e c o n d 3 ∘ . For simplicity let the radius of the disc be 3 0 c m so the ant walks at 1 s e c c m
The time for the ant to cross the chord must be the same as the time for the far end of the chord to rotate to the other side.
Let the central angle formed by the chord to be θ . The chord must rotate 1 8 0 ∘ − θ which it will do in ( 6 0 − 3 θ ) s e c
The chord has length 6 0 sin 2 θ c m which will take the ant 6 0 sin 2 θ s e c
Equate these times and solve to get θ = 7 2 . 9 7 6 ∘ which equates to approximately 3 6 s e c o n d s