The area is almost whole.

Two circles of radius 5 are separated by 1 unit. The shaded area is almost a whole number, but is actually slightly less than a whole number.
If A is the actual area then the error ϵ = ⌈ A ⌉ − A .
It turns out ϵ 1 itself is very close to a whole number. Enter this whole number.
You might start with the inspiration for this problem.
The answer is 30.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
pi/2 instead of pi, but the end result is the same
I'll commit a venial sin and post a calculus solution to a geometry problem. Say R = 5 and D = 1 . The two circles are:
x 2 + y 2 = R 2 ( x − D ) 2 + y 2 = R 2 y 1 = R 2 − x 2 y 2 = R 2 − ( x − D ) 2
It is fairly easy to determine that the intersection between the two circles occurs at x = 2 D . Half of the shaded area is therefore equal to:
2 A = ∫ D / 2 R 2 ( y 2 − y 1 ) d x + ∫ R R + D 2 y 2 d x
This yields:
A ≈ 1 9 . 9 6 6 6 1 6 5 ϵ 1 ≈ 2 9 . 9 5 4 9
That is my method also, approximation makes me feel unsure about the answer...
It's a correct solution with a valid process, and for me, that is no mathematical sin. I tried for a while to reason out the geometric argument on paper, and I just couldn't get it to where I needed it to be. I finally threw the circle equations into Desmos graphing calculator, and the tool did enough low-level stuff for me that I could reason my way through the high-level stuff. Generally, I feel satisfied having discovered the correct answer, as long as my method was sound.
Below is a picture showing the centers of the circles and the place where the regions almost overlap. It is turned sideways from the original drawing above. The centers of the circles are A and B so A B = 1 and A D = 5
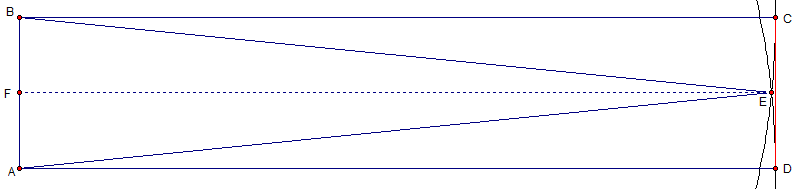
The error is the area of four copies a little almost-triangle C E D but with two curved sides. The area of this triangle can found by taking rectangle A B C D and subtracting triangle A E B and the two sectors C B E and D A E .
A B = 1 , A D = 5 so the area of rectangle A B C D is 5
E F is the leg of triangle A F E . 0 . 5 2 + E F 2 = 5 2 so E F = 2 3 1 1 . Area of triangle A E B = 4 3 ⋅ 1 1
The sectors have central angle sin − 1 ( 1 / 1 0 ) and so each has an area π ⋅ 5 2 ⋅ 3 6 0 ∘ sin − 1 ( 1 / 1 0 )
So the area of the one almost-triangle is
5 − 2 ⋅ π ⋅ 2 5 ⋅ 3 6 0 ∘ sin − 1 ( 1 / 1 0 ) − 4 3 ⋅ 1 1 ≈ 0 . 0 0 8 3 4 5 8 7 8 2
The error is four of these so ϵ = 0 . 0 3 3 3 8 3 5 1 2 8 and ϵ 1 = 2 9 . 9 5 4 9 0 6 3 6 which is very close to the whole number 3 0
Thanks for posting this. It let me revisit my work on the previous problem and realize I made the mistake of ( 5 − cos θ ) 2 = 2 5 − 2 cos θ + cos 2 θ which turns out multiplying the error by about 5 7 times @_@. Nice problem.
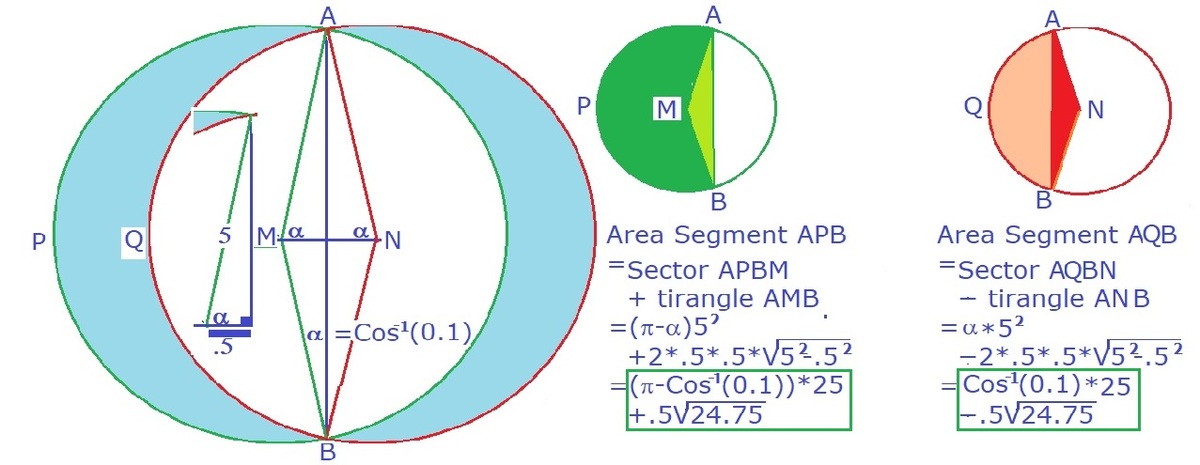 T
o
t
a
l
a
r
e
a
o
f
t
w
o
b
l
u
e
r
e
g
i
o
n
=
2
∗
{
S
e
g
m
e
n
t
(
A
P
B
)
−
S
e
g
m
e
n
t
(
A
Q
B
)
}
=
2
∗
{
(
π
−
2
∗
C
o
s
−
1
(
.
1
)
)
∗
2
5
+
2
4
.
7
5
}
=
1
9
.
9
6
6
6
.
.
.
.
.
≈
2
0
.
∴
ϵ
=
2
0
−
1
9
.
9
6
6
6
.
.
.
.
ϵ
1
=
2
9
.
9
5
4
9
.
T
h
e
r
e
q
u
i
r
e
d
a
n
s
w
e
r
=
3
0
.
T
o
t
a
l
a
r
e
a
o
f
t
w
o
b
l
u
e
r
e
g
i
o
n
=
2
∗
{
S
e
g
m
e
n
t
(
A
P
B
)
−
S
e
g
m
e
n
t
(
A
Q
B
)
}
=
2
∗
{
(
π
−
2
∗
C
o
s
−
1
(
.
1
)
)
∗
2
5
+
2
4
.
7
5
}
=
1
9
.
9
6
6
6
.
.
.
.
.
≈
2
0
.
∴
ϵ
=
2
0
−
1
9
.
9
6
6
6
.
.
.
.
ϵ
1
=
2
9
.
9
5
4
9
.
T
h
e
r
e
q
u
i
r
e
d
a
n
s
w
e
r
=
3
0
.
Consider the first quadrants of the two circles. Let A and B be the centers of the two circles, therefore, A B = 1 , and A C = 5 and B D = 5 be their radius on the x -axis. Point P is where the two circles intersect and O be the mid-point of A B . By symmetry, O P is perpendicular to A B .
The shaded area [ P C D ] ( [ ⋅ ] denotes the area) is given by:
[ P C D ] ⟹ A ϵ ⟹ ϵ 1 = [ O P D ] − [ O P C ] = [ B P D ] + [ O P B ] − ( [ A P C ] − [ O P A ] ) = 2 5 2 ( π + θ ) + 2 5 2 sin θ cos θ − 2 5 2 ( π − θ ) + 2 5 2 sin θ cos θ = 2 5 ( θ + sin θ cos θ ) = 2 5 ( sin − 1 0 . 1 + 0 . 1 1 − 0 . 1 2 ) = 4 × 2 5 ( sin − 1 0 . 1 + 0 . 1 1 − 0 . 1 2 ) ≈ 1 9 . 9 6 7 = ⌈ A ⌉ − A ≈ 2 0 − 1 9 . 9 6 7 = 0 . 0 3 3 = 0 . 0 3 3 1 ≈ 3 0 Note that sin θ = 5 2 1 = 0 . 1