The Area Of My Heart
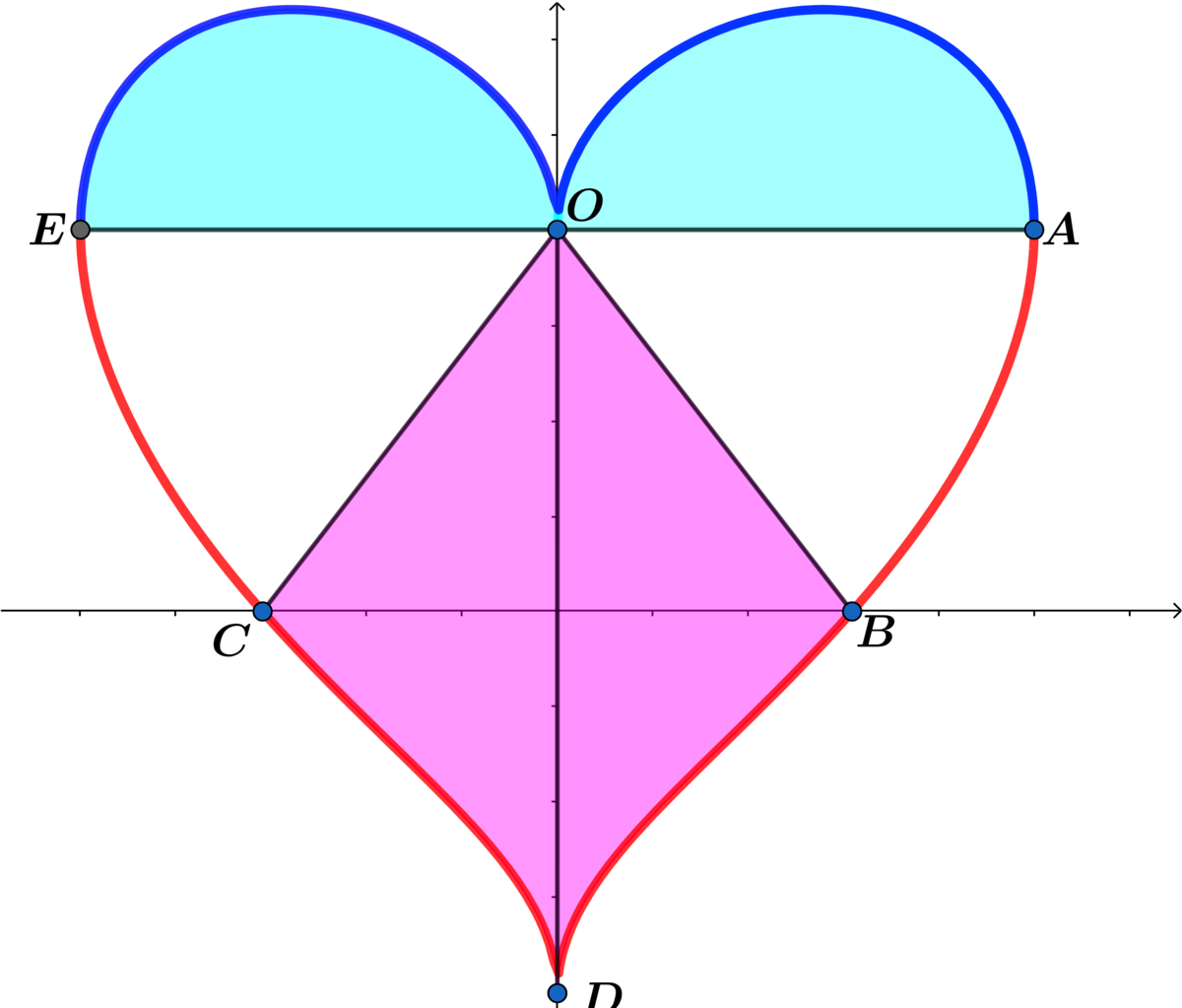
In the heart curve x 2 + ( 4 5 y − ∣ x ∣ ) 2 = 1 above, O B goes from the positive y intercept to the positive x intercept and O C goes from the positive y intercept to the negative x intercept and points O , B , D , C encloses the pink region.
The enclosed blue region is bounded by the upper portion of the curve x 2 + ( 4 5 y − ∣ x ∣ ) 2 = 1 and the line A E .
Let A T o t a l be the total area of the blue and pink region as described above.
If A T o t a l can be expressed as b a 2 ( arcsin ( ϕ − 1 ) − c 1 ( ϕ − 1 ) a c + ( ϕ − 1 ) + a π − c a ) , where a , b and c are coprime positive integers and ϕ is the golden ratio, find a + b + c .
The answer is 10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
For the red region:
For the x intercept of y 1 = 5 4 ( x − 1 − x 2 ) we obtain:
x 2 + x − 1 = 0 ⟹ x = 2 − 1 ± 5 , since x = − 2 1 + 5 = − ϕ results in a complex valued square root ⟹ x = 2 5 − 1 is the x intercept of y 1 = 5 4 ( x − 1 − x 2 ) .
The equation of the line passing thru O : ( 0 , 5 4 ) and B : ( 2 5 − 1 , 0 ) is:
y = 5 4 ( 5 − 1 − 2 x + 1 ) ⟹
A r e d = 5 4 ∫ 0 2 5 − 1 ( 1 − 5 − 1 2 x + 1 − x 2 − x ) d x
For ∫ 1 − x 2 d x
Let x = sin ( θ ) ⟹ d x = cos ( θ ) ⟹ ∫ 1 − x 2 d x = ∫ cos 2 ( θ ) d θ = 2 1 ( θ + sin ( θ ) cos ( θ ) ) .
Let β = 2 5 − 1
⟹ ∫ 0 2 5 − 1 1 − x 2 d x = 2 1 arcsin ( β ) + 2 1 β 2 3 ⟹ A r e d = 5 4 ( 2 1 arcsin ( β ) + 2 1 β 2 3 + ( − 3 2 x 2 3 + x − 5 − 1 x 2 ) ∣ 0 2 5 − 1 ) = 5 2 ( arcsin ( β ) − 3 1 β 2 3 + β )
β = 2 5 − 1 = 2 1 + 5 − 1 = ϕ − 1 ⟹ A r e d = 5 2 ( arcsin ( ϕ − 1 ) − 3 1 ( ϕ − 1 ) 2 3 + ϕ − 1 ) ⟹ A 1 = 2 A r e d = 5 4 ( arcsin ( ϕ − 1 ) − 3 1 ( ϕ − 1 ) 2 3 + ϕ − 1 )
For blue region:
A b l u e = 5 4 ∫ 0 1 ( 1 − x 2 + x − 1 ) d x
L e t x = sin ( θ ) ⟹ d x = cos ( θ ) d θ ⟹
A b l u e = 5 4 ( 2 1 ( θ + 2 1 sin ( 2 θ ) ) ∣ 0 2 π + ( 3 2 x 2 3 − x ) ∣ 0 1 ) ) = 5 4 ( 4 π − 3 1 )
A 2 = 2 A b l u e = 5 8 ( 4 π − 3 1 )
⟹
A T o t a l = A 1 + A 2 = 5 4 ( arcsin ( ϕ − 1 ) − 3 1 ( ϕ − 1 ) 2 3 + ϕ − 1 + 2 π − 3 2 ) =
b a 2 ( arcsin ( ϕ − 1 ) − c 1 ( ϕ − 1 ) a c + ( ϕ − 1 ) + a π − c a ) ⟹
a + b + c = 1 0 .