Heron? Shoelace? Varignon's? Brahmagupta's?

In the square shown, the areas of the white triangles are 7, 9, and 11.
What is the area of the shaded triangle?
Give your answer to 2 decimal places.
The answer is 21.84032967.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
my same method :)
Similar approach ......just different variables :D :D
My process was too long. I took two variables, and then solved a bi-quadratic, however, the answer was correct. But this is a nice solution. I didn't think it this way first, i started thinking it in a complex fashion LOL!!
Didn't take the time to solve it algebraically, thought someone would have a quicker answer. Anyone notice the triangle labeled 7 is bigger than the triangle labelled 9?
Lots of algebra, but it's all straighforward.
Let a be the side of the square, b the horizontal side of the 7-triangle, and c the vertical side of the 9-triangle. We write equations representing the given areas:
a b = 1 4 , a c = 1 8 , ( a − b ) ( a − c ) = a 2 − a c − a b + b c = 2 2 The last equation simplifies to a 2 − 1 8 − 1 4 + a 2 1 4 × 1 8 = 2 2 , s o a 4 − 5 4 a 2 + 2 5 2 = 0 . We find a 2 = 2 7 ± 3 5 3 , but we reject the solution with the negative sign as being too small; we need a 2 > 7 + 9 + 1 1 .
The area we seek is ( 2 7 + 3 5 3 ) − 7 − 9 − 1 1 = 3 5 3 ≈ 2 1 . 8 4
Same, it's easier to solve in this way

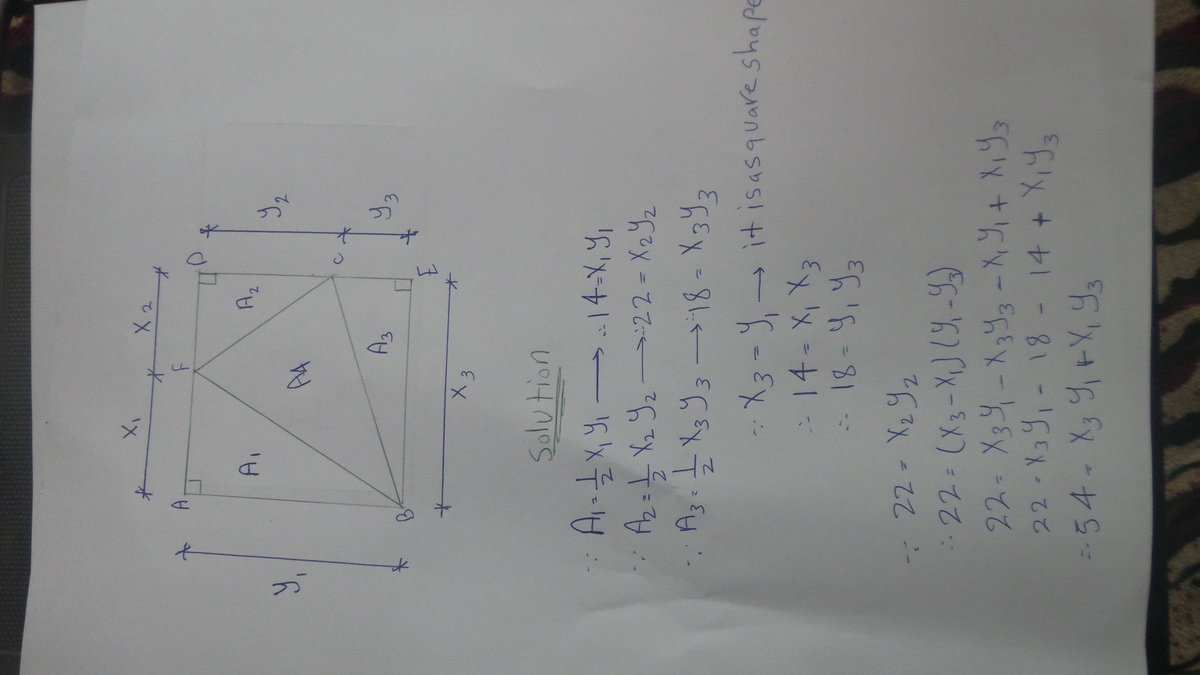 I solved it in this photo i hope that can help you :]
I solved it in this photo i hope that can help you :]
There is a wonderful generalization of the solution for this problem: A = √[(a + b + c)^2 - 4ac] Where “a,” “b,” and “c” are the known areas, and “A” is the unknown area. Caveat: “a” and “c’ must be the triangles whose long legs are the side of the square, in this case 7 and 9. A = √[27x27 - 4(9x7)] = √(729 - 252) = 21.84
I solve this problem by using C programming and answer is 21.840330

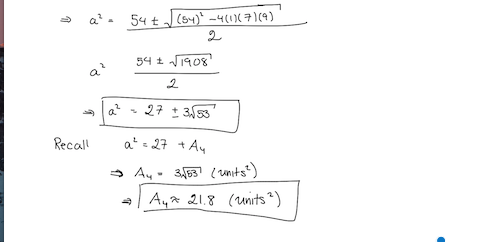
Let each side of the square ABED be x .
Therefore, the area of the square ABED = x 2 .
As we know that the Area of a triangle = Δ = 2 1 B a s e ∗ H e i g h t
Δ A B C = 2 1 A C ∗ A B = 7 ⇒ A C = x 1 4 ⇒ D C = x − x 1 4 Δ B E F = 2 1 B E ∗ E F = 9 ⇒ E F = x 1 8 ⇒ D F = x − x 1 8 Δ C D F = 2 1 D C ∗ D F = 1 1 ⇒ ( x − x 1 4 ) ( x − x 1 8 ) = 2 2 ⇒ x 4 − 5 4 x 2 + 2 5 2 = 0 The above is a quadratic equation in x 2 , therefore, x 2 = 2 7 ± 3 5 3 The Area of the Required Shaded Region is the Area of the Square - Sum of the Area of the 3 Given Triangles.
Therefore, Required Area of Shaded Region = x 2 − 2 7 = 2 7 ± 3 5 3 − 2 7 = ± 3 5 3 = + 3 5 3 ≡ 2 1 . 8 4
The negative sign is abandoned as Area cannot be Negative. :D