The area was lost. Please find it.
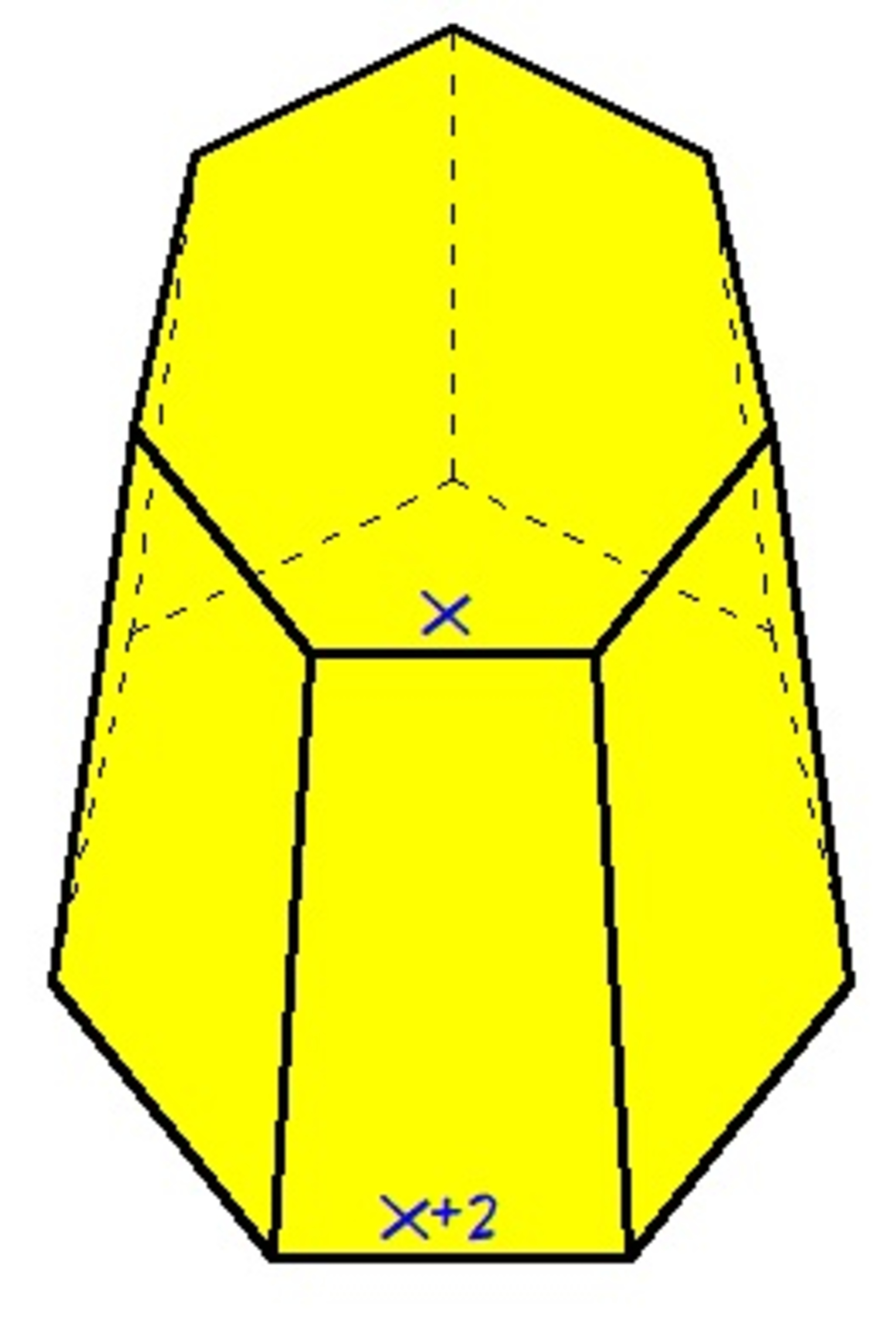 The lateral area of the truncated right pyramid shown above is
. The upper base is a regular heptagon with edge length of
. The lower base is a regular heptagon with edge length of
. If the perpendicular distance between the bases is
, find the sum of the base areas rounded to the nearest integer.
The lateral area of the truncated right pyramid shown above is
. The upper base is a regular heptagon with edge length of
. The lower base is a regular heptagon with edge length of
. If the perpendicular distance between the bases is
, find the sum of the base areas rounded to the nearest integer.
The answer is 573.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Extend the seven slant edges to meet at the vertex V of the non-truncated pyramid. Let h be the distance from the midpoint of an x + 2 side to that vertex. Then the height of each trapezium forming the sides is x + 2 2 h , and so the lateral area is L = 7 × 2 1 ( x + x + 2 ) × x + 2 2 h = x + 2 1 4 ( x + 1 ) h If d ( x ) is the distance from the midpoint of a heptagon of side x to the centre, then d ( x ) = 2 1 x cot 7 π , and the vertical height of the vertex V above the base is H = h 2 − d ( x + 2 ) 2 = 1 4 ( x + 1 ) x + 2 L 2 − 4 9 ( x + 1 ) 2 cot 2 7 π so the vertical height of the frustrum of the pyramid is K = x + 2 2 H = 7 ( x + 1 ) 1 L 2 − 4 9 ( x + 1 ) 2 cot 2 7 π and hence ( x + 1 ) 2 = 4 9 ( K 2 + cot 2 7 π ) L 2 The sum of the areas of the two heptagons is 7 [ 2 1 x d ( x ) + 2 1 ( x + 2 ) d ( x + 2 ) ] = 4 7 ( x 2 + ( x + 2 ) 2 ) cot 7 π = 2 7 ( ( x + 1 ) 2 + 1 ) cot 7 π = 2 tan 7 π 7 [ 4 9 ( K 2 + cot 2 7 π ) L 2 + 1 ] With K = 9 and L = 6 3 8 2 , we obtain 5 7 3 . 1 0 7 6 as the sum of the heptagonal areas, which makes the answer 5 7 3 .