The Areas of A Half-Circle and A Combined Shape
A half-circle with radius r has an area equal to that of a combined shape with a half-circle of radius r − 1 and a rectangle of height 3 π .
What is
r
?
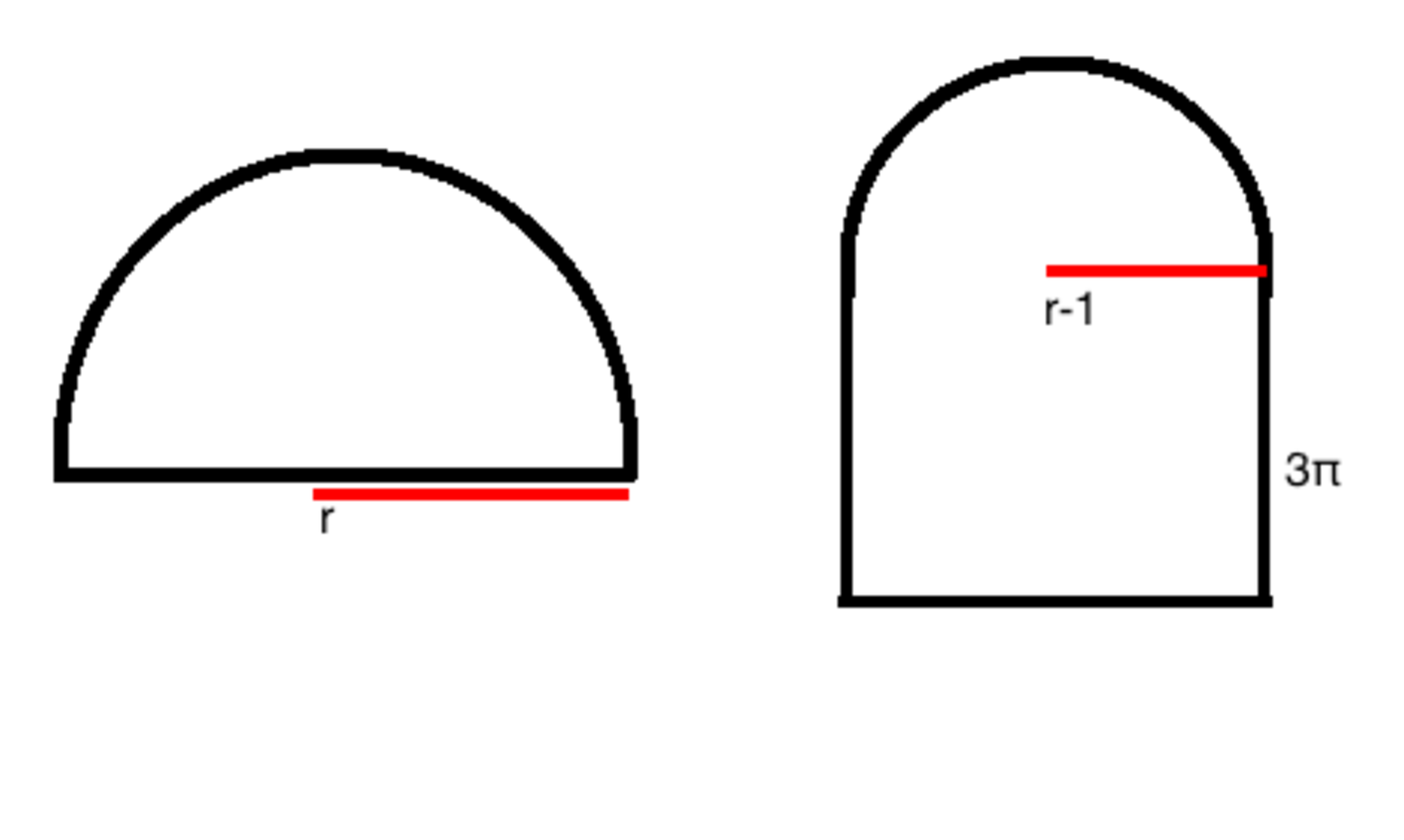
The answer is 1.1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
solving for the area of the semi-circle:
A = 2 1 π r 2
solving for the area of the composite figure:
The base of the rectangle is ( r − 1 ) + ( r − 1 ) = 2 r − 2 . Therefore, the area is 3 π ( 2 r − 2 )
The area of the semi-circle above the rectangle is 2 1 π ( r − 1 ) 2 .
solving for "r":
Equating both areas (because both areas are equal), we have
2 1 π r 2 = 3 π ( 2 r − 2 ) + 2 1 π ( r − 1 ) 2
π cancels out
2 1 r 2 = 3 ( 2 r − 2 ) + 2 1 ( r − 1 ) 2
2 1 r 2 = 3 ( 2 r − 2 ) + 2 1 ( r 2 − 2 r + 1 )
2 1 r 2 = 6 r − 6 + 2 1 r 2 − r + 2 1
2 1 r 2 cancels out
0 = 6 r − 6 − r + 2 1
5 . 5 = 5 r
Dividing both sides by 5 , we have
1 . 1 = r
or
r = 1 . 1 answer
Since the areas are equal, we have
2 π r 2 = 2 π ( r − 1 ) 2 + 3 π ( 2 ) ( r − 1 )
2 r 2 = 2 1 ( r 2 − 2 r + 1 ) + 6 r − 6
2 r 2 = 2 r 2 − r + 2 1 + 6 r − 6
6 r − r = 6 − 2 1
5 r = 5 . 5
r = 1 . 1
The semicircle with radius r has an area equal to 2 π r 2 .
The composite shape has an area equal to the sum of the areas of the semicircle and the rectangle which is = 2 π ( r − 1 ) 2 + 2 ( r − 1 ) ⋅ 3 π = 2 π ( r − 1 ) 2 + 6 π ( r − 1 ) .
Equating both areas, we get
⟹ ⟹ ⟹ ⟹ 2 π r 2 r 2 r 2 0 r = = = = = 2 π ( r − 1 ) 2 + 6 π ( r − 1 ) ( r − 1 ) 2 + 1 2 ( r − 1 ) r 2 − 2 r + 1 + 1 2 r − 1 2 1 0 r − 1 1 1 0 1 1 = 1 . 1