The Art of Zig-zag Geometry

Geometry Level 3

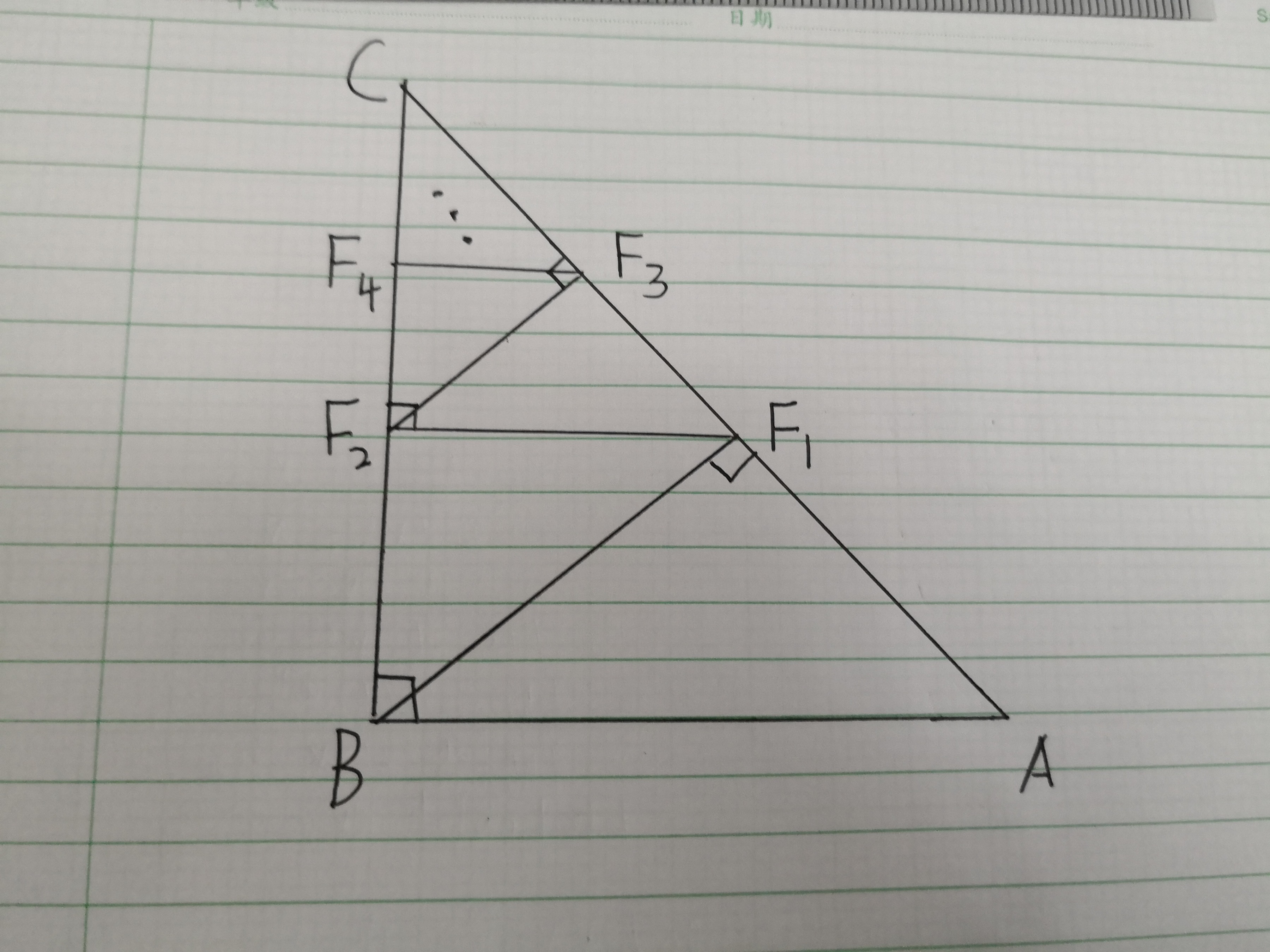
Given a triangle Δ A B C \Delta ABC with ∠ A B C \angle ABC = 9 0 ∘ 90^{\circ} and ∣ A B ∣ = 15 , ∣ B C ∣ = 20 , ∣ A C ∣ = 25 |AB|=15, |BC|=20, |AC|=25 , From B, a perpendicular line is drawn to A C AC such that the perpendicular foot on AC is at F 1 F_{1} . From F 1 F_{1} , a perpendicular line is drawn from F 1 F_{1} to B C BC such that the perpendicular foot on BC is at F 2 F_{2} . The similiar process continues up to n n times such that n n → \rightarrow ∞ \infty . Let the sum of areas of Δ B F 1 F 2 \Delta BF_{1}F_{2} , Δ F 2 F 3 F 4 \Delta F_{2}F_{3}F_{4} , Δ F 4 F 5 F 6 \Delta F_{4}F_{5}F_{6} , ..., and Δ F 2 n − 2 F 2 n − 1 F 2 n \Delta F_{2n-2}F_{2n-1}F_{2n} be S x S_x and the area of Δ A B C \Delta ABC be S t S_t . If S x S t \cfrac{S_x}{S_t} = a b \cfrac{a}{b} such that a a and b b are co-prime positive integers, then find a + b a+b .

This is part of the set Fun With Problem-Solving .


The answer is 57.

Donglin Loo by donglin loo , 22, Singapore

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Donglin Loo
Jan 24, 2018

Let A F 1 = h AF_{1}=h and ∠ B A C = θ \angle BAC=\theta

cos ⁡ θ = 15 25 = 3 5 \cos \theta=\cfrac{15}{25}=\cfrac{3}{5}

cos ⁡ θ = h 15 \cos \theta=\cfrac{h}{15}

h 15 = 3 5 \cfrac{h}{15}=\cfrac{3}{5}

h = 9 h=9

So, A F 1 = 9 , C F 1 = 16 AF_{1}=9, CF_{1}=16

A r e a o f Δ A B F 1 A r e a o f Δ C B F 1 = A F 1 C F 1 = 9 16 \cfrac {Area of \Delta ABF_{1}}{Area of \Delta CBF_{1}}=\cfrac{AF_{1}}{CF_{1}}=\cfrac{9}{16}

A r e a o f Δ C B F 1 A r e a o f Δ A B C = 16 25 \cfrac {Area of \Delta CBF_{1}}{Area of \Delta ABC}=\cfrac{16}{25}

S i n c e F 1 F 2 ⊥ B C , Since F_{1}F_{2}\perp BC,

F 1 F 2 ∥ B A F_{1}F_{2}\parallel BA

Δ F 1 F 2 C ∼ Δ A B C \Delta F_{1}F_{2}C\sim \Delta ABC

C F 2 C B = C F 1 C A = 16 25 \cfrac{CF_{2}}{CB}=\cfrac{CF_{1}}{CA}=\cfrac{16}{25}

A r e a o f Δ B F 1 F 2 A r e a o f Δ C F 1 B = F 2 B C B = F 1 A C A = 9 25 \cfrac{Area of \Delta BF_{1}F_{2}}{Area of \Delta CF_{1}B}=\cfrac{F_{2}B}{CB}=\cfrac{F_{1}A}{CA}=\cfrac{9}{25}

A r e a o f Δ B F 1 F 2 A r e a o f Δ A B C = A r e a o f Δ B F 1 F 2 A r e a o f Δ C F 1 B ⋅ A r e a o f Δ C F 1 B A r e a o f Δ A B C = 9 25 ⋅ 16 25 \cfrac{Area of \Delta BF_{1}F_{2}}{Area of \Delta ABC}=\cfrac{Area of \Delta BF_{1}F_{2}}{Area of \Delta CF_{1}B}\cdot\cfrac{Area of \Delta CF_{1}B}{Area of \Delta ABC}=\cfrac{9}{25}\cdot\cfrac{16}{25}

S i n c e Δ F 1 F 2 C ∼ Δ A B C , Since \Delta F_{1}F_{2}C\sim \Delta ABC,

A r e a o f Δ F 1 F 2 C A r e a o f Δ A B C = ( F 1 C A C ) 2 = ( 16 25 ) 2 \cfrac{Area of \Delta F_{1}F_{2}C}{Area of \Delta ABC}=(\cfrac{F_{1}C}{AC})^{2}=(\cfrac{16}{25})^{2}

It follows that Δ B F 1 F 2 ∼ Δ F 2 F 3 F 4 , Δ F 2 F 3 F 4 ∼ Δ F 4 F 5 F 6 , . . . , Δ F 2 n − 4 F 2 n − 3 F 2 n − 2 ∼ Δ F 2 n − 2 F 2 n − 1 F 2 n \Delta BF_{1}F_{2}\sim \Delta F_{2}F_{3}F_{4}, \Delta F_{2}F_{3}F_{4}\sim \Delta F_{4}F_{5}F_{6}, ..., \Delta F_{2n-4}F_{2n-3}F_{2n-2}\sim \Delta F_{2n-2}F_{2n-1}F_{2n}

From above, A r e a o f Δ B 1 F 2 A r e a o f Δ A B C = 9 25 ⋅ 16 25 \cfrac{Area of \Delta B_{1}F_{2}}{Area of \Delta ABC}=\cfrac{9}{25}\cdot\cfrac{16}{25}

⇒ A r e a o f Δ B F 1 F 2 = 9 25 ⋅ 16 25 ⋅ A r e a o f Δ A B C \Rightarrow Area of \Delta BF_{1}F_{2}=\cfrac{9}{25}\cdot\cfrac{16}{25}\cdot Area of \Delta ABC

A r e a o f Δ F 2 F 3 F 4 = ( 16 25 ) 2 ⋅ A r e a o f Δ B F 1 F 2 = ( 16 25 ) 2 ⋅ 9 25 ⋅ 16 25 ⋅ A r e a o f Δ A B C Area of \Delta F_{2}F_{3}F_{4}=(\cfrac{16}{25})^{2}\cdot Area of \Delta BF_{1}F_{2}=(\cfrac{16}{25})^{2}\cdot\cfrac{9}{25}\cdot\cfrac{16}{25}\cdot Area of \Delta ABC

A r e a o f Δ F 4 F 5 F 6 = ( 16 25 ) 2 ⋅ A r e a o f Δ F 2 F 3 F 4 = ( 16 25 ) 4 ⋅ 9 25 ⋅ 16 25 ⋅ A r e a o f Δ A B C Area of \Delta F_{4}F_{5}F_{6}=(\cfrac{16}{25})^{2}\cdot Area of \Delta F_{2}F_{3}F_{4}=(\cfrac{16}{25})^{4}\cdot\cfrac{9}{25}\cdot\cfrac{16}{25}\cdot Area of \Delta ABC

..............................................................

A r e a o f Δ F 2 n − 2 F 2 n − 1 F 2 n = ( 16 25 ) 2 ⋅ A r e a o f Δ F 2 n − 3 F 2 n − 2 F 2 n − 1 = ( 16 25 ) 2 n − 2 ⋅ 9 25 ⋅ 16 25 ⋅ A r e a o f Δ A B C Area of \Delta F_{2n-2}F_{2n-1}F_{2n}=(\cfrac{16}{25})^{2}\cdot Area of \Delta F_{2n-3}F_{2n-2}F_{2n-1}=(\cfrac{16}{25})^{2n-2}\cdot\cfrac{9}{25}\cdot\cfrac{16}{25}\cdot Area of \Delta ABC

A r e a o f Δ B F 1 F 2 + A r e a o f Δ F 2 F 3 F 4 + A r e a o f Δ F 4 F 5 F 6 + . . . A r e a o f Δ F 2 n − 2 F 2 n − 1 F 2 n = A r e a o f Δ A B C ⋅ 9 25 ⋅ 16 25 ⋅ ( ( 16 25 ) 0 + ( 16 25 ) 2 + ( 16 25 ) 4 + . . . + ( 16 25 ) 2 n − 2 ⏟ n t e r m s ) Area of \Delta BF_{1}F_{2}+Area of \Delta F_{2}F_{3}F_{4}+Area of \Delta F_{4}F_{5}F_{6}+...Area of \Delta F_{2n-2}F_{2n-1}F_{2n}=Area of \Delta ABC\cdot \cfrac{9}{25}\cdot\cfrac{16}{25}\cdot(\underbrace{(\cfrac{16}{25})^{0}+(\cfrac{16}{25})^{2}+(\cfrac{16}{25})^{4}+...+(\cfrac{16}{25})^{2n-2}}_{n terms})

S x = 9 25 ⋅ 16 25 ⋅ ( ( 16 25 ) 0 + ( 16 25 ) 2 + ( 16 25 ) 4 + . . . + ( 16 25 ) 2 n − 2 ) ⏟ n t e r m s ⋅ S t S_{x}=\cfrac{9}{25}\cdot\cfrac{16}{25}\cdot(\underbrace{(\cfrac{16}{25})^{0}+(\cfrac{16}{25})^{2}+(\cfrac{16}{25})^{4}+...+(\cfrac{16}{25})^{2n-2})}_{n terms}\cdot S_{t}

S x S t = 9 25 ⋅ 16 25 ⋅ ( ( 16 25 ) 0 + ( 16 25 ) 2 + ( 16 25 ) 4 + . . . + ( 16 25 ) 2 n − 2 ) ⏟ n t e r m s \cfrac{S_{x}}{S_{t}}=\cfrac{9}{25}\cdot\cfrac{16}{25}\cdot(\underbrace{(\cfrac{16}{25})^{0}+(\cfrac{16}{25})^{2}+(\cfrac{16}{25})^{4}+...+(\cfrac{16}{25})^{2n-2})}_{n terms}

S x S t \cfrac{S_{x}}{S_{t}} = 9 25 ⋅ 16 25 ⋅ ( 16 25 ) 0 × ( 1 − ( 16 25 ) 2 n ) 1 − ( 16 25 ) 2 \cfrac{9}{25}\cdot\cfrac{16}{25}\cdot\cfrac{(\cfrac{16}{25})^{0}\times(1-(\cfrac{16}{25})^{2n})}{1-(\cfrac{16}{25})^{2}}

As n → ∞ n\rightarrow\infty

S x S t \cfrac{S_{x}}{S_{t}} = 9 25 ⋅ 16 25 ⋅ ( 16 25 ) 0 × ( 1 − 0 ) 1 − ( 16 25 ) 2 \cfrac{9}{25}\cdot\cfrac{16}{25}\cdot\cfrac{(\cfrac{16}{25})^{0}\times(1-0)}{1-(\cfrac{16}{25})^{2}}

S x S t \cfrac{S_{x}}{S_{t}} = 9 25 ⋅ 16 25 ⋅ 1 1 − ( 16 25 ) 2 \cfrac{9}{25}\cdot\cfrac{16}{25}\cdot\cfrac{1}{1-(\cfrac{16}{25})^{2}}

S x S t \cfrac{S_{x}}{S_{t}} = 9 25 ⋅ 16 25 ⋅ 1 ( 1 − 16 25 ) ( 1 + 16 25 ) \cfrac{9}{25}\cdot\cfrac{16}{25}\cdot\cfrac{1}{(1-\cfrac{16}{25})(1+\cfrac{16}{25})}

S x S t \cfrac{S_{x}}{S_{t}} = 9 25 ⋅ 16 25 ⋅ 1 ( 9 25 ) ( 41 25 ) \cfrac{9}{25}\cdot\cfrac{16}{25}\cdot\cfrac{1}{(\cfrac{9}{25})(\cfrac{41}{25})}

S x S t \cfrac{S_{x}}{S_{t}} = ⋅ 16 25 ⋅ 1 41 25 \cdot\cfrac{16}{25}\cdot\cfrac{1}{\cfrac{41}{25}}

S x S t \cfrac{S_{x}}{S_{t}} = 16 41 \cfrac{16}{41}

1 Helpful 0 Interesting 0 Brilliant 0 Confused

Lol I entered the other surface and thought:whaaaaat? So I checked the answer and it turned out I did everything right.... I didn't use the cosine at start. The equivalence of the triangles followed quickly to me by the fact 2 of 3 angles are always the sane here(for instance by using Z-angle)

Peter van der Linden - 3 years, 4 months ago

What do u mean by other surface?

donglin loo - 3 years, 4 months ago
Rab Gani
Jun 6, 2018

Triangles ΔABC, ΔBF1F2, ΔF1F2F3, are similar.By similarity : AC/BC = AB/BF1, So we can find BF1=12. By the same way, we can find F1F2=9.6, BF2=7.2,and F2F3=7.68. ΔBF1F2, ΔF1F2F3,...form geometric progression with tha ratio r = (7.68/12)^2 = (16/25)^2. We can find Sx = (9.6)(3.6)/[1 – (16/25)^2] = (3.84)(625)/41 The area of ΔABC, St = 150. So Sx/St = 16/41., and a+b=57

0 Helpful 0 Interesting 0 Brilliant 0 Confused

@rab gani

You can use LaTeX to beautify your answer or question. Use "\" with "(" to start and use "\" with ")" to end it. We apply on variables (such as ), number (), point (point , line ). This is the basic use of :

https://brilliant.org/profile/chan-n20gy9/sets/latex/485571/beginner-latex-guide/

For instance, the solution you proposed, when written in LaTeX becomes:

Triangles Δ A B C , Δ B F 1 F 2 , Δ F 1 F 2 F 3 , \Delta ABC,\Delta BF_{1}F_{2}, \Delta F_{1}F_{2}F_{3}, are similar.

By similarity : A C B C = A B B F 1 \cfrac{AC}{BC} = \cfrac{AB}{BF_{1}} ,

So we can find B F 1 = 12 BF_{1}=12 .

By the same way, we can find F 1 F 2 = 9.6 F_{1}F_{2}=9.6

B F 2 = 7.2 BF_{2}=7.2 and F 2 F 3 = 7.68 F_{2}F_{3}=7.68 .

Δ B F 1 F 2 , Δ F 1 F 2 F 3 \Delta BF_{1}F_{2}, \Delta F_{1}F_{2}F_{3} ,...form geometric progression with the ratio r = ( 7.68 / 12 ) 2 = ( 16 / 25 ) 2 r = (7.68/12)^2 = (16/25)^2 .

We can find S x = ( 9.6 ) ( 3.6 ) / [ 1 − ( 16 / 25 ) 2 ] = ( 3.84 ) ( 625 ) / 41 S_{x} = (9.6)(3.6)/[1 - (16/25)^2] = (3.84)(625)/41

The area of Δ A B C , S t = 150 \Delta ABC, S_{t} = 150 .

So S x S t = 16 41 \cfrac{S_{x}}{S_{t}}= \cfrac{16}{41} ., and a + b = 57 a+b=57

donglin loo - 3 years ago

Log in to reply

Thank's a lot for your comments and suggestion.

rab gani - 3 years ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...