The beauty of circles - part I
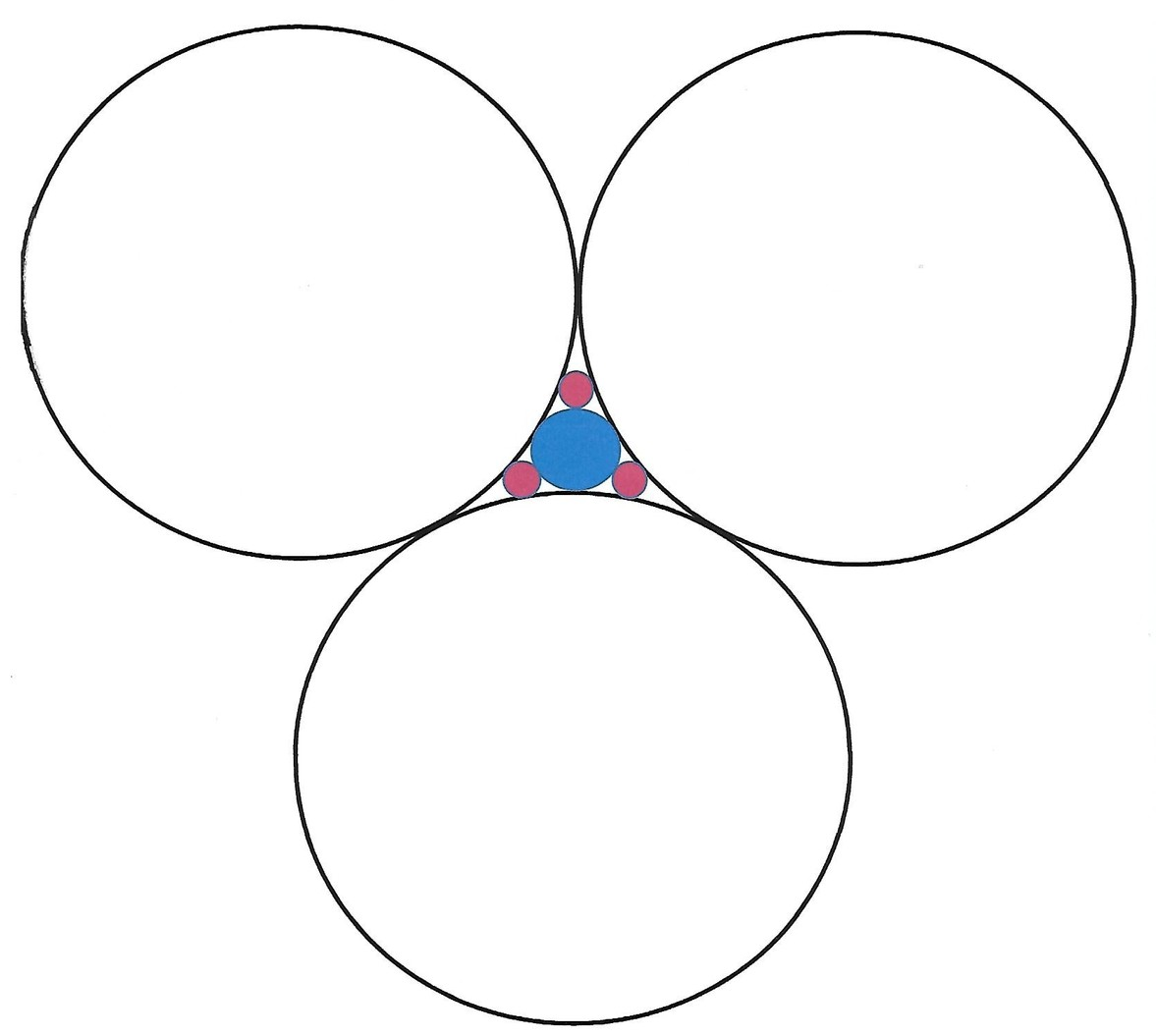
As shown in the figure above, the three white circles with the same radius R are tangent to each other and with a blue circle with radius p . Each of the three red circles with the same radius r is tangent to two white circles and the blue circle. Then
R r = d a − b c
where a , b , c , and d are positive integers such that g cd ( a , b , d ) = 1 and c is square-free. Find a + b + c + d .
The answer is 49.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Definitely using such powerful formula is the shortest way to solve the problem.
Did the same way. Cheers :-)
This problem has a quick solution using circle inversion. More details here , but for the purposes of this problem the key facts about circle inversion through a unit circle centred at a point O are
- a point P maps to point P ′ , where P ′ lies on the line connecting O P , and O P ⋅ O P ′ = 1
- a circle passing through O maps to a straight line not passing through O
- a circle not passing through O maps to a circle not passing through O
- tangency is preserved
Take as the centre of inversion the point of tangency between the two green circles ( O ). The diagram has the original setup on the left (recoloured and with just one of the smaller circles), and the result of the inversion on the right.
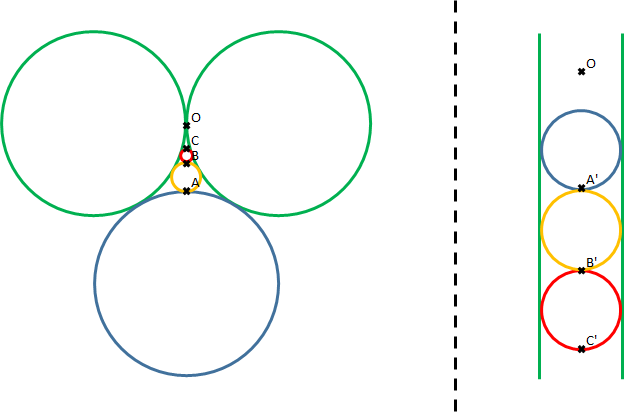
The two green circles map to two parallel lines, separated by a distance R 1 (to see this, consider what happens to the points on the green circles furthest from O under inversion.)
Any circle that is tangent to both green circles in the original diagram is tangent to both green lines in the inversion, so must be sandwiched between them. But this includes the blue, yellow and red circles. In the inversion these all have the same diameter, R 1 .
To find r , we just need to work out the distance B C . Since the centres of the large circles form an equilateral triangle of side 2 R , we have:
O A O A ′ O B ′ O C ′ = ( 3 − 1 ) R = ( 3 − 1 ) R 1 = 2 R 3 + 1 = O A ′ + R 1 = 2 R 3 + 3 = O B ′ + R 1 = 2 R 3 + 5
Inverting back, this gives
O B O C B C R r = 3 + 3 2 R = 3 + 5 2 R = 2 r = 3 + 3 2 R − 3 + 5 2 R = 3 3 2 R ( 9 − 4 3 ) = 3 3 9 − 4 3
giving the answer 9 + 4 + 3 + 3 3 = 4 9
Quite unusual approach! Impressive.
W L O G l e t R = 1 . L e t t h e c e n t e r o f t h e t h r e e w h i t e c i r c l e s b e A , B , C , a n d t h e c e n t e r o f t h e b l u e c i r c l e b e O . T h e n Δ A B C i s e q u i l a t e r a l a n d i t s c i r c u m c e n t e r ( a l s o i t s c e n t r o i d ) i s t h e c e n t e r o f t h e b l u e c i r c l e . T h e d i s t a n c e f r o m a v e r t e x t o t h e c i r c u m c e n t e r = 3 2 ∗ ( i t s a l t i t u d e ) . ∴ A O = B O = C O = 3 2 ∗ 3 ∗ R = 3 2 . B u t A O = R + p = 1 + p . ⟹ p = 3 2 − 1 ⟹ p 1 = 3 2 − 1 1 . ∴ p 1 = 3 + 2 ∗ 3 . A p p l y i n g D e c a r t e ′ s T h e o r e m t o c i r c l e s c e n t e r s A , B , O , r 1 = 1 + 1 + ( 3 + 2 ∗ 3 ) + 2 ∗ 2 ( 3 + 2 ∗ 3 ) + 1 . ∴ . r 1 = 5 + 2 3 + 2 7 + 4 ∗ 3 = 5 + 2 3 + 2 ( 2 + 3 ) 2 = 9 + 4 ∗ 3 . ⟹ R r = 1 r = r = 9 + 4 ∗ 3 1 = 8 1 − 4 8 9 − 4 ∗ 3 = 3 3 9 − 4 ∗ 3 = d a − b ∗ c . ∴ a + b + c + d = 9 + 4 + 3 + 3 3 = 4 9 .
Let the centers of the three white circles be A , B , and C , and the center of the blue circle be O . Then △ A B C is equilateral and its centroid is the center of the blue circle O . The distance from a vertex to centroid is 3 2 its altitude, therefore A O = B O = C O = 3 2 × 3 R = 3 2 R . Note that A O = R + p = 3 2 R ⟹ p = ( 3 2 − 1 ) R .
Let the center of a red circle nearer to A be P . Then ∠ A O P = 6 0 ∘ . By cosine rule, we have:
A P 2 ( R + r ) 2 R 2 + 2 r R + r 2 2 r R ( 3 R − p ) r r ⟹ R r = O P 2 + A O 2 − 2 ( O P ) ( A O ) cos ∠ A O P = ( p + r ) 2 + ( R + p ) 2 − 2 ( p + r ) ( R + p ) × 2 1 = p 2 + 2 p r + r 2 + R 2 + 2 p R + p 2 − ( p 2 + p r + p R + r R ) = p 2 + p r + p R + p 2 − r R = p ( R + p ) = ( 3 R − p ) p ( R + p ) = 4 R − ( R + p ) p ( R + p ) = 4 R − 3 2 R ( 3 2 − 1 ) R × 3 2 R = 1 2 − 2 3 2 ( 2 − 3 ) R = 6 − 3 2 − 3 = 3 3 9 − 4 3 Recall p = ( 3 2 − 1 ) R and R + p = 3 2 R
Therefore, a + b + c + d = 9 + 4 + 3 + 3 3 = 4 9 .
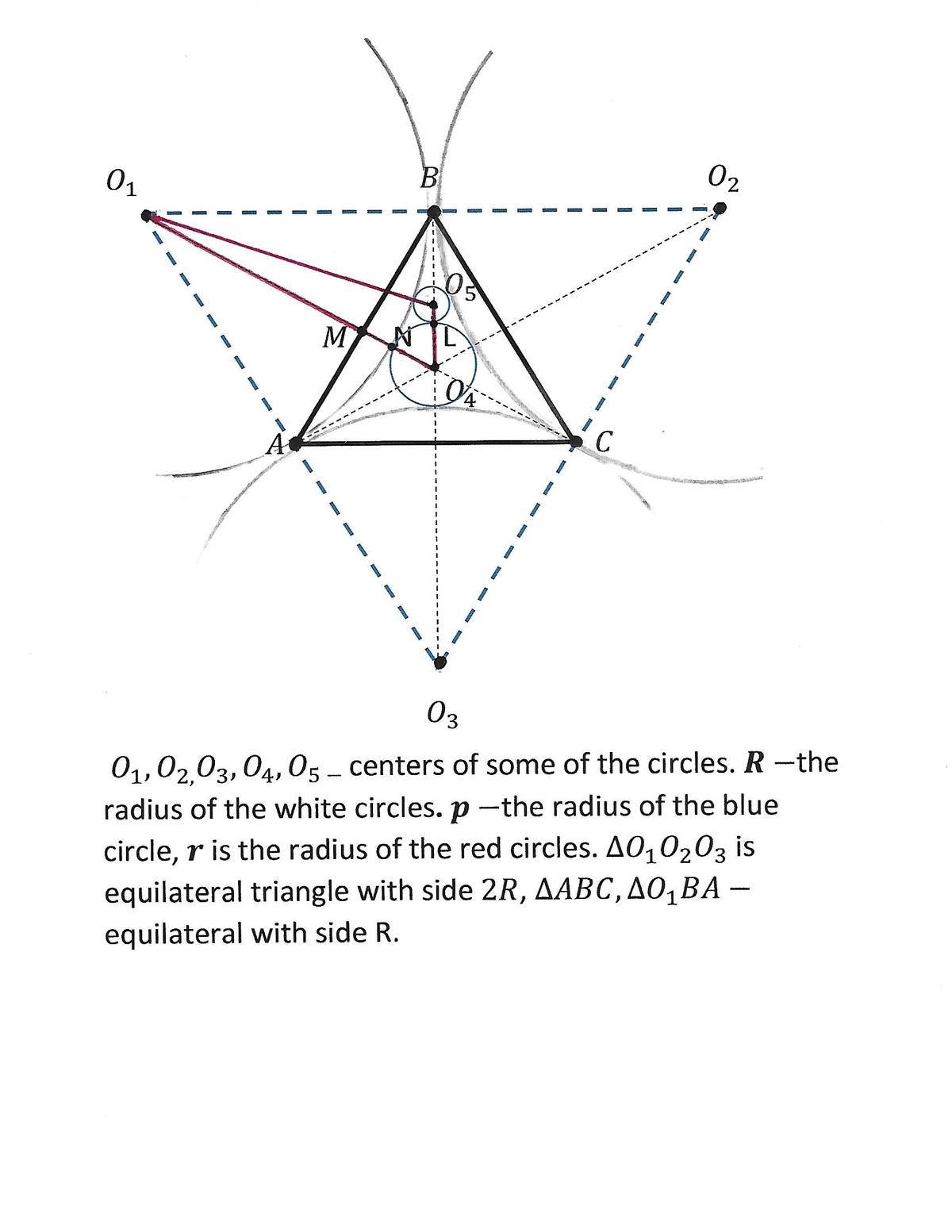

Using Descartes' Circle Theorem on the one blue and three white circles, p 1 = R 1 + R 1 + R 1 + R 1 R 1 + R 1 R 1 + R 1 R 1 , which simplifies to p 1 = R 3 + 2 3 .
Using Descartes' Circle Theorem on the one red, one blue, and two white circles, r 1 = p 1 + R 1 + R 1 + p 1 R 1 + R 1 R 1 + p 1 R 1 , which after substituting the above expression for p 1 simplifies to r 1 = R 9 + 4 3 , which further rearranges to R r = 3 3 9 − 4 3 .
Therefore, a = 9 , b = 4 , c = 3 , and d = 3 3 , and a + b + c + d = 4 9 .