The beauty of circles - part II

Geometry Level 4

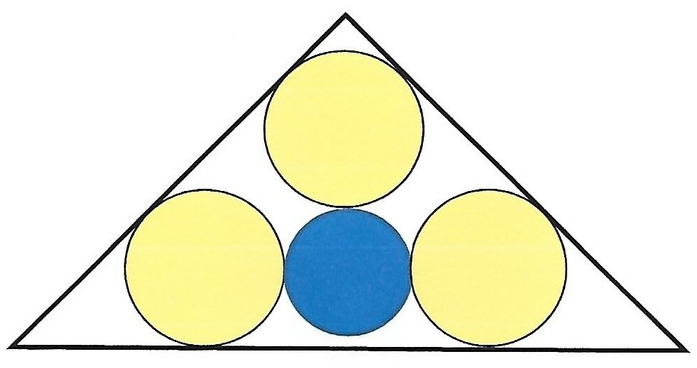
An isosceles right triangle is with a leg equal to $\sqrt{2}$ . Three yellow circles with the same radius are drawn inside the triangle, each one tangent to the sides of a different inside angle without overlapping with the other circles. A fourth blue circle not necessarily with the same radius is drawn inside the triangle, tangent to the yellow circles. The sum of the absolute minimum and the absolute maximum of the total of the areas of the four circles has the following form:

$\large \frac{a-b\sqrt{c}}{d}\pi$

where $a$ , $b$ , $c$ and $d$ are positive integers such that $\gcd(a,b,d)=1$ and $c$ is square-free. Find $a+b+c+d$ .

The answer is 202.

2 solutions

Chew-Seong Cheong
Dec 2, 2018

Let the radius of the yellow circles be $x$ and the radius of the blue circle be $y$ . From the figure above, we find that $x$ and $y$ is related as $(2+\sqrt 2) x + y = 1$ $\implies y = 1 - (2+\sqrt 2)x$ , and the total area of the four circles is given by:

$\begin{aligned} A & =3 \pi x^2 + \pi y^2 & \small \color{#3D99F6} \text{Recall }y = 1 - (2+\sqrt 2)x \\ \implies & = \pi \left((9+4\sqrt 2)x^2 - (4+2\sqrt 2)x + 1\right) \\ & = \pi (9+4\sqrt 2)\left(x^2 - \frac {4+2\sqrt 2}{9+4\sqrt 2}x + \frac 1{9+4\sqrt 2} \right) \\ & = \pi \left((9+4\sqrt 2){\color{#3D99F6}\left(x - \frac {2+\sqrt 2}{9+4\sqrt 2}\right)^2} + \frac 3{9+4\sqrt 2} \right) \end{aligned}$

Since $\left(x - \dfrac {2+\sqrt 2}{9+4\sqrt 2}\right)^2 \ge 0$ , $A$ is minimum when $\left(x - \dfrac {2+\sqrt 2}{9+4\sqrt 2}\right) = 0$ . $\implies A_{min} = \dfrac {3\pi}{9+4\sqrt 2} = \dfrac {27-12\sqrt 2}{49}\pi$ .

And $A$ is maximum when $\left(x - \dfrac {2+\sqrt 2}{9+4\sqrt 2}\right)$ is maximum or $x$ is maximum. $x$ is maximum when the top yellow circle is tangent to the bottom two yellow circles. Then we have

$\begin{aligned} (2x)^2 & = (x+y)^2 + (x+y)^2 \\ \implies 2x & = \sqrt 2(x+y) \\ y & = (\sqrt 2 -1)x & \small \color{#3D99F6} \text{Recall }y = 1 - (2+\sqrt 2)x \\ \implies x & = \frac 1{1+2\sqrt 2} = \frac {2\sqrt 2-1}7 \end{aligned}$

And we have:

$\begin{aligned} A_{max} & = \pi \left((9+4\sqrt 2)\left(\frac {2\sqrt 2-1}7 - \frac {2+\sqrt 2}{9+4\sqrt 2}\right)^2 + \frac 3{9+4\sqrt 2} \right) \\ & = \pi \left(\frac {(\sqrt 2-1)^2}{9+4\sqrt 2} + \frac 3{9+4\sqrt 2} \right) = \frac {6-2\sqrt 2}{9+4\sqrt 2} \pi \\ & = \frac {70-42\sqrt 2}{49} \pi \end{aligned}$

Therefore, $A_{min}+A_{max} = \dfrac {27-12\sqrt 2}{49}\pi + \dfrac {70-42\sqrt 2}{49} \pi = \dfrac {97-54\sqrt 2}{49} \pi$ , implying $a+b+c+d=97+54+2+49 = \boxed{202}$ .