The biggest triangle
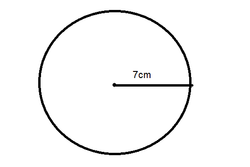 What is the biggest area of a triangle can be drawn inside a circle along the radius of 7?
What is the biggest area of a triangle can be drawn inside a circle along the radius of 7?
The answer is 63.65286718.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
There is a much simpler solution which studies the function
2 7 2 ( sin θ 1 + sin θ 2 + sin θ 3 ) .
Log in to reply
Would you please elaborate:
- How do we get to that function?
- How do we proceed after having it?
Log in to reply
Step 1: It is obvious that the triangle should contain the point O (or be on the boundary). Otherwise, we could adjust a base down, which increases the length of the base and the height of the triangle, thereby increasing it's area.
Step 2: Given any triangle ABC, define ∠ A O B = θ 1 , ∠ B O C = θ 2 , ∠ C O A = θ 3 . Then, we have θ 1 + θ 2 + θ 3 = 2 π . From step 1, all of these angles are from 0 to π .
Step 3: The area of ABC is given by
2 7 2 ( sin θ 1 + sin θ 2 + sin θ 3 )
Step 4: Observe that sin θ is a concave function on [ 0 , π ] . Hence, by Jensen's Inequality , it follows that the maximum is achieved at θ 1 = θ 2 = θ 3 = 3 2 π .
Step 5: Conclude that this gives us the equilateral triangle.
nice solution :)
Log in to reply
Thanks for a fun problem.
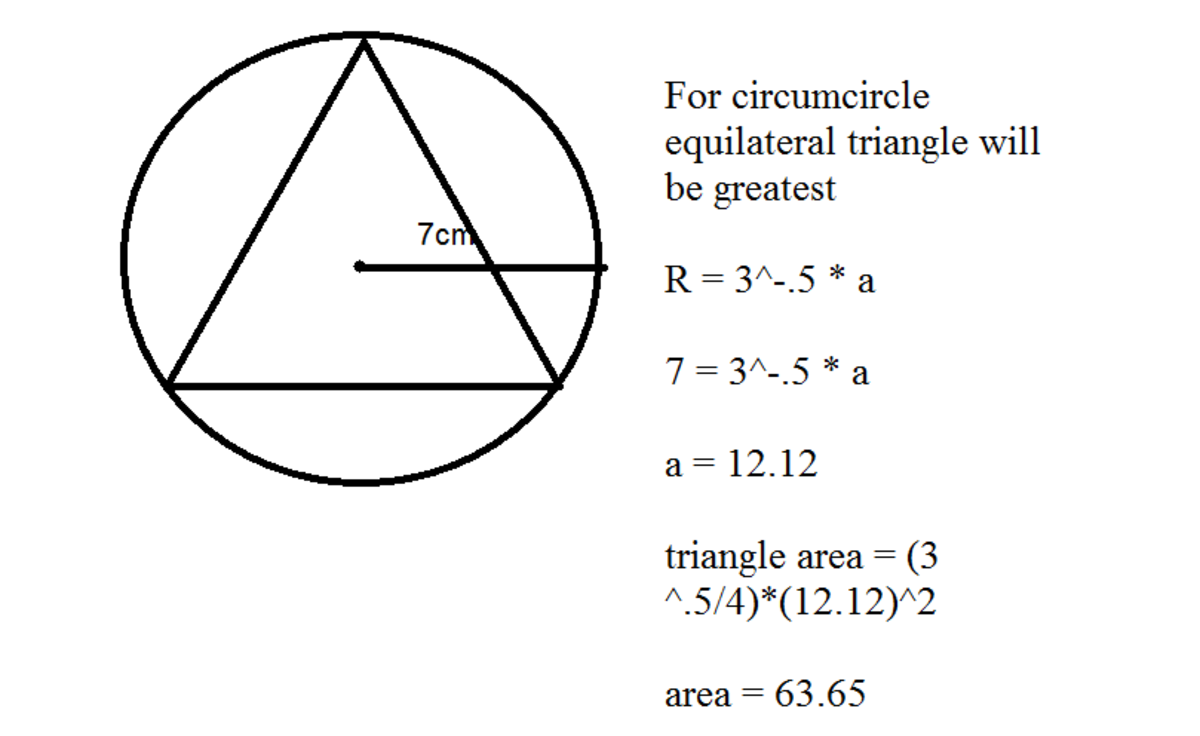
Here is a general triangle, circumscribed in a circle of radius r . Additional markings have been made to help us solve the problem.
Note that we can choose any one side as a base, because the circle is symmetrical from all angles of viewing.
Also note: 0 ≤ h 1 , h 2 ≤ r .
Let us find the width, w , and the height h , of this triangle, so that we can find a formula for the area, A .
Height is simple, h = h 1 + h 2 .
To find width, we need to use the Pythagorean theorem,
r 2 = h 1 2 + ( w / 2 ) 2 ⇒ w / 2 = r 2 − h 1 2 ⇒ w = 2 r 2 − h 1 2 .
Thus we see that
A = 2 ( h 1 + h 2 ) ⋅ 2 r 2 − h 1 2 = ( h 1 + h 2 ) r 2 − h 1 2 .
Note that h 2 is not affected by h 1 , so we are free to set it to its maximum value, r .
A = ( h 1 + r ) r 2 − h 1 2 .
So now we have a formula describing A . Now we will use some calculus to find its maximum value.
Since A 2 will have the same maximum as A , and is a little easier to differentiate, we will use it to find our critical points (where d h 1 d ( A 2 ) = 0 ).
Squaring, A 2 = ( h 1 + r ) 2 ( r 2 − h 1 2 ) .
Taking the derivative,
d h 1 d ( A 2 ) = 2 ( h 1 + r ) ( r 2 − h 1 2 ) − 2 h 1 ( h 1 + r ) 2
Factoring out 2 ( h 1 + r ) ,
= 2 ( h 1 + r ) [ ( r 2 − h 1 2 ) − h 1 ( h 1 + r ) ] = 2 ( h 1 + r ) [ r 2 − h 1 2 − h 1 2 − h 1 r ] = 2 ( h 1 + r ) [ r 2 − h 1 r − 2 h 1 2 ]
Factoring again,
= 2 ( h 1 + r ) ( r − 2 h 1 ) ( r + h 1 ) = 2 ( r + h 1 ) 2 ( r − 2 h 1 ) .
Thus we see that d h 1 d ( A 2 ) = 0 when h 1 = r / 2 (the other values of h 1 are not between 0 and r ).
To find the absolute maximum value of A , therefore, we must check h 1 = r / 2 , as well as the bounds of h 1 = 0 and h 1 = 1 .
A ∣ h 1 = 0 = ( 0 + r ) r 2 − 0 2 = r ⋅ r = r 2 .
A ∣ h 1 = r / 2 = ( r / 2 + r ) r 2 − ( r / 2 ) 2 = ( 3 r / 2 ) r 1 − 1 / 4 = ( 3 r 2 / 2 ) 3 / 4 = ( 3 r 2 / 4 ) 3 = ( 3 3 / 4 ) r 2 .
A ∣ h 1 = r = ( r + r ) r 2 − r 2 = 0 .
Since, ( 3 3 / 4 ) r 2 > r 2 > 0 , we see that A reaches an absolute maximum of ( 3 3 / 4 ) r 2 at h 1 = r / 2 .
Plugging in r = 7 , we see that the maximum area is ( 3 3 / 4 ) ( 7 ) 2 ≈ 6 3 . 6 5 3 .
QED.