The Blue One!

Geometry Level 3

A B C D ABCD is a square with side length of 4 cm 4 \text{ cm} . Four quarter-circles are drawn with vertices of the square as their centres and radius 4 cm 4 \text{ cm} as shown in the figure. What is the area of the blue region (to 3 decimal places)?

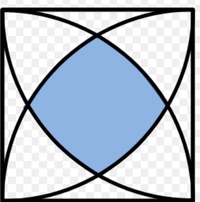
Bonus: Use geometry.


The answer is 5.042.

Mr. India by Mr. India , 17, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Chew-Seong Cheong
Mar 29, 2019

Due to symmetry we can consider one quarter of the blue area as shown in the figure.

A blue 4 = Area of 3 0 ∘ circle sector − Area of isosceles triangle (red lines) + Area of right triangle = 30 360 × π ( 4 2 ) − 1 2 ( 4 2 ) sin ⁡ 3 0 ∘ + 1 2 ( 4 sin ⁡ 6 0 ∘ − 2 ) 2 = 4 π 3 − 4 + 8 − 4 3 ⟹ A blue = 16 π 3 + 16 − 16 3 ≈ 5.042 \begin{aligned} \frac {A_{\color{#3D99F6}\text{blue}}}4 & = \text{Area of }30^\circ \text{ circle sector} - \text{Area of isosceles triangle (red lines)} + \text{Area of right triangle} \\ & = \frac {30}{360}\times \pi (4^2) - \frac 12(4^2) \sin 30^\circ + \frac 12 \left(4\sin 60^\circ - 2\right)^2 \\ & = \frac {4\pi}3 - 4 + 8 - 4\sqrt 3 \\ \implies A_{\color{#3D99F6}\text{blue}} & = \frac {16\pi}3 + 16 - 16\sqrt 3 \approx \boxed{5.042} \end{aligned}

1 Helpful 0 Interesting 1 Brilliant 1 Confused

Just brilliant! Better than the way I did.

Mr. India - 2 years, 2 months ago

How do we prove that angle is 30° ?

Mr. India - 1 year, 8 months ago

Log in to reply

The bottom two vertices of the square and the point where the two arcs cross on top form an equilateral triangle. This means that the angle between the left side of the square and the left red line is 3 0 ∘ 30^\circ . Similarly, the angle between the bottom of the square and the bottom red line is also 3 0 ∘ 30^\circ . Then the angle between the two red lines is 9 0 ∘ − 3 0 ∘ − 3 0 ∘ = 3 0 ∘ 90^\circ - 30^\circ - 30^\circ = 30^\circ .

Chew-Seong Cheong - 1 year, 8 months ago

The area is four times the area of one fourth of the blue region bounded by one of the quadrants of circles, and the lines joining the mid points of the sides of the square. This is 16π/3-16(√3-1).

1 Helpful 0 Interesting 0 Brilliant 0 Confused

Can you please elaborate more?

Mr. India - 2 years, 2 months ago

Log in to reply

It is very difficult for me to type sign of integration, draw a curve and so on. This is a big limitation I have. Join the mid points of the opposite sides of the square to divide the blue region into four congruent regions. Find the point of intersection of two quadrants of circles as (2,2√3). Use integration technique to calculate the area. I think you will understand my limitation. Thank you.

A Former Brilliant Member - 2 years, 2 months ago

Log in to reply

Oh you used integration! Actually I don't yet know about it that's why the bonus question is there.

Thank you for posting it

Suggestion : you can also write on paper and click photo as solution

Mr. India - 2 years, 2 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...