The bouncing ball
I've posted a question, so to celebrate, I decided to play pool. Somehow my house has tables with holes at four corners of any dimensions. The ball and the holes are negligibly small (epsilon by epsilon).
My mathematical friend says, "I will give you a m × n rectangular table where m , n are positive integers summing to 2015. It's up to me to decide. Hahaha. Then we will play." Then he will put the ball at one corner.
I am very bad at aiming, so I only have a machine that will shoot the ball at an angle of 45° to the sides of the table. My evil friend wants the ball to bounce as many times as possible before it reaches any hole so that the ball can lose as much kinetic energy as possible and leave me in suspense.
I calculate that the maximum number of bounces is M .
For how many ordered pairs ( m , n ) does the number of bounces equal M ?
Clarifications:
As an explicit example, a 1 × 2 table needs 1 bounce, and a 2 × 3 table needs 3 bounces. A 1 × 2 0 1 4 table needs 2013 bounces.
You may make the assumption that we are decent mathematicians, although we can't play pool and do weird things. Note also that this is combinatorics, not computer science.
The answer is 1440.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions

Although it is true, why does (m, n) have to be 1?
Log in to reply
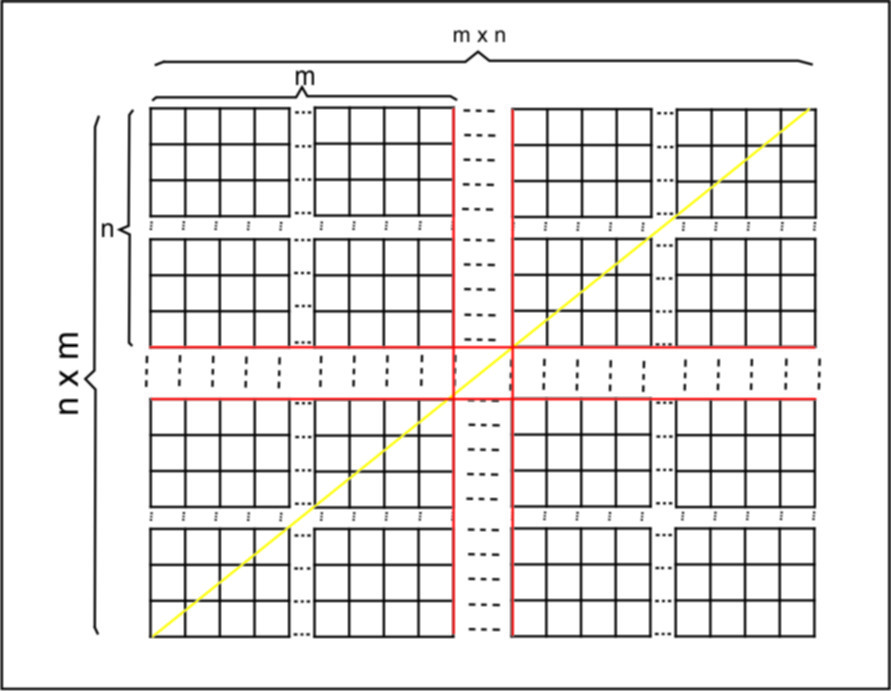
You make a square with length side is m x n. This square made by m x n of m x n rectangular (paint this side by red color) . You draw a yellow diagonal of this square. The number of point meet by the yellow line and red line is the bounce of ball.
Consider the rectangular lattice generated by ( m , 0 ) and ( 0 , n ) . The line y = x represents the path of the ball on a series of (possibly reflected) images of the pool table. Bouncing off a wall corresponds to crossing over one of the sides of one of the fundamental rectangles.
The ball goes into the hole at ( m a , n b ) where m a = n b and a and b are the minimum positive solutions to this equation. Clearly a = n / d , b = m / d where d = g c d ( m , n ) . The ball bounces a + b − 2 times. In order to maximize this, we should have d = 1 and so M = 2 0 1 3 . The answer is the number of ( m , n ) such that m + n = 2 0 1 5 and g c d ( m , n ) = 1 , which is equivalent to g c d ( m , 2 0 1 5 ) = 1 , so it's φ ( 2 0 1 5 ) = 1 4 4 0 .
Nice solution!
Imagine the ball lies in any corner and is hit at an angle of 4 5 ° . After some distance it will reach a wall and bounce back. Now imagine you mirrored the pool table on the side where it bounced back - on the mirrored table, the ball follows the same line it had been on before (also see Vu Van Luan's solution)!
Notice: By mirroring the table along the side where a bounce occurs, the ball rolls along a line of the form ( x , y ) = t ( ± 1 , ± 1 ) , t ∈ R (signs depend on the initial direction the ball was hit to).
Notice: The corners of the mirrored m × n -table lie at ( k m , l n ) , k , l ∈ Z
Now let's find the number of bounces B ≤ M . The ball reaches a hole of the (mirrored) table if ( x , y ) = ! ( k m , l n ) ⇒ ± k m = ! ± l n ⇒ ( k m , l n ) = z l c m ( m , n ) ⋅ ( ± 1 , ± 1 ) , z ∈ Z ( ∗ ) We need the solution where the ball reaches a hole for the first time , i.e. z = 1 . The number of bounces against the horizontal and vertical walls until the ball reaches a hole are l − 1 , k − 1 respectively. We need to subtract one as there is no bouncing back when the ball reaches the hole: B = l + k − 2 ( ∗ ) = m l c m ( m , n ) + n l c m ( m , n ) − 2 = g cd ( m , n ) m + n − 2 = g cd ( m , n ) N − 2 ≤ N − 2 ∣ l c m ( m , n ) ⋅ g cd ( m , n ) = m n ∣ m + n = N : = 2 0 1 5 We really can get the maximum number of bounces (consider an 1 × ( N − 1 ) -table), so the maximum number of bounces is M = N − 2 . Using m + n = N , we find g cd ( m , n ) = g cd ( m , N − m ) = g cd ( m , N )
Notice: We get the maximum number of bounces if (and only if) g cd ( m , n ) = g cd ( m , N ) = 1
We can count the number of tables with maximum bounce by counting the numbers 1 ≤ m ≤ N with g cd ( m , N ) = 1 . That number is given by φ ( N ) = 4 ⋅ 1 2 ⋅ 3 0 = 1 4 4 0
Let m be on x -axis and n on y -axis.
Then we can see that ball has to travel n L C M ( m , n ) on x -axis and m L C M ( m , n ) on y -axis
Then the number of bounces on side m = n L C M ( m , n ) − 1 .
Similarly, number of bounces on side n = m L C M ( m , n ) − 1 .
∴ Total number of bounces = ( n L C M ( m , n ) − 1 ) + ( m L C M ( m , n ) − 1 ) = L C M ( m , n ) ( m 1 + n 1 ) − 2
⟹ Total Bounces = H C F ( m , n ) m n m n ( m + n ) − 2
⟹ Total Bounces = H C F ( m , n ) 2 0 1 5 − 2
∴ For maximum bounces H C F ( m , n ) = 1 and M = 2 0 1 3 .
1 = H C F ( m , n ) = H C F ( m , 2 0 1 5 − m ) = H C F ( m , 2 0 1 5 )
⟹ # m = ϕ ( 2 0 1 5 ) = 1 4 4 0
∴ Number of solutions = 1 4 4 0 .