The cake is a liar!
Alan, Ben, Chris, Dave and Emma are eating a big cake. After eating, there was one slice left, and they decided to leave it for Frank but someone ate it! Frank knows that these 5 people are each telling one truth and one lie:
Alan says, "It wasn't Emma. It was Ben."
Ben says, "It wasn't Chris. It wasn't Emma."
Chris says, "It was Emma. It wasn't Alan."
Dave says, "It was Chris. It was Ben."
Emma says, "It was Dave. It wasn't Alan."
Who ate the last slice of cake?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
26 solutions
Look at statements 2 and 4. You'll find the answer in the shortest possible way to answer.
Ben: it wasn't Chris. It wasn't Emma.
Dave: It was Chris. It was Ben.
Among the two statements given by Ben one should be true and the other should be false. If it wasn't chris, then it should be Emma. But in Dave's statement also, one should be true and the other should be wrong. If it was Emma, then both the statements will be wrong. So it was CHRIS.
Log in to reply
nice answer
I agree that that's the simplest way. I set up a quick chart and those two stuck out.
That's how I solved it.
Yes so the logic is faulty based on Dave's claims? I agree that the rest of the info points to Chris
B R A V O !
Consider third and fifth statements if it was not Alan then it was Emma by third statement by fifth statement it was Dave how can both eat a single piece so it was alan
Log in to reply
From the question: "Frank knows that each of these 5 people are each telling one truth and one lie" Going by that, "it wasn't Alan" can't be the truth in either of the statements (as it would make the other statement in the pair true, i.e, 3rd statement will have "It was Emma", and 5th will have "It was Dave" as the true statements which contradict each other so they both are false.) So, "It wasn't Alan" is the truth, which can be used to eliminate Alan, Dave and Emma from the list of suspects and use the other statements (1st,2nd,4th) to further break down the list of suspects to one person.
Nice job :D
From Dave's statement, we can tell either Ben or Chris ate the cake. If Ben ate the cake we find that both the statements Alan and Ben were true which are unacceptable. Therefore, Chris ate the cake and we find that the statements of each person is one true one false.
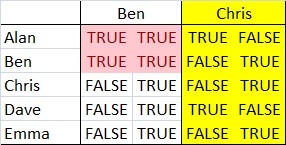
Moderator note:
Of course, one could create the full table and compare which column has 1 True/False in each row. Noticing Dave's statement allows us to focus on just these 2 columns.
Ben states that "It wasn't Chris" and "It wasn't Emma." Because each person tells one truth and one lie, we know that either Chris or Emma ate the cake. Applying the same reasoning to Dave's statements, we know that either Chris or Ben ate the cake. Both dichotomies point to Chris having eaten the cake.
This was exactly what i did. Faster and simpler.
I will refer to Alan as A, Ben as B, Chris as C, Dave as D and Emma as E (to keep things simple). I solved it by assuming a person's two statements as one being the truth and the other being a lie. And I start by A's statement.
If we assume 'It wasn't Emma' to be a lie and 'It was Ben' as the truth, then this implies that both Ben and Emma ate the piece of the cake, but we know that only one person ate the cake. So, 'It wasn't Emma' must be the truth and 'It was Ben' must be a lie.
Then by examining the statements of B, we see that 'It wasn't Chris' must be a lie and 'It wasn't Emma' must be the truth. So at this stage, it seems as if C is the one who ate the cake.
If we analyse C's statements, according to our deductions before, 'It was Emma' must be a lie and 'It wasn't Alan' must be the truth. At this point, C still seems to be the main suspect.
Moving on to Dave's statements, 'It was Ben' must be a lie and 'It was Chris' should be the truth.
Finally, by thinking about Emma's statements, one can conclude that, 'It was Dave' is a lie and 'It wasn't Alan' to be the truth. These conclusions have to be made in order for our assumptions to be true.
Thus, in the end, it is clear that Chris is the real culprit. If there is an error in my reasoning, please comment!! :)
We can also assume one by one the 5 members as the culprits and then check the 5 statements and make sure in each statement there is one lie and one truth. Only in the case of Chris, each of the statements have one truth and one lie.
If you read the statements before assuming anything and just follow simple logic, you notice that Ben says 2 people didn't eat it, meaning one of these people did it.
You also notice that Dave says that 2 people did eat the cake. Meaning it was also one of these people.
The common name between the 2 is Chris, therefore it was Chris.
The easy way: One of Dave's statements was true, so it's either Chris or Ben. But, since Ben is not an option (the multiple choice said Brian), it must be Chris.
Since one of them HAS to be a lie and one HAS to be the truth, you can reverse everyone to make them say "It wasn't x, it wasn't x" by simply putting the "It was" statement as false. Two of them have the same statement though, Ben and Dave. Since ben says "It wasn't", one of them is a lie and it must be "It was", the opposite goes for Dave that says "It was", one of them is the truth, so you match the only single name in both of their answers (Chris) and here you go!
Answer : Chris ate the missing cake.
The unique thing about this puzzle is the uniformity, that each of them is telling one truth and one lie consistently. So, if we heard statements with 2 accusations or 2 denials (as long as the two are of the same nature), then we can be sure that the lone criminal name will make an appearance in both (because one of the accusations has to be the truth and one of the denials has to be false). So, gathering information from Dave's 2 accusations and Ben's 2 denials, we heard that Chris' name is mentioned by both, so he is the guilty party here.
Set up 2 cases per person, one where the first statement is true & second is false, then switch. There are 3 cases where the individual outcomes lead to the impossible situation of 2 people being guilty. Use these people’s alternate cases to mark A, B, C, D & E not guilty where result shows this. This leaves only 1 possible guilty person.
Ben says: "It wasn't Chris, It wasn't Emma", since one of these statements must be false, either Chris or Emma did it.
Alan says: "It wasn't Emma, It was Ben." Since we already know Ben couldn't have done it, that is the lie. therefore his other statement , "It wasn't Emma" must be a truth.
Since it was either Chris or Emma, and it wasn't Emma, then it must've been Chris.
Analyzing Ben's statement led to 2 possibilities: either it was Chris or Emma. Analyzing Dave's statement led to 2 possibilities: either it was Chris or Ben.
Therefore it was Chris
It's easy to determine which statement must be true for Emma, Chris, and Alan, as the only way for the one-truth, one-lie rule to hold is if each of their wasn't is true, otherwise they'd be saying 2 different people ate the cake, which would break the one-cake-eater rule.
By removing all those wasn't s as options - the only possibility left is Chris.
Since the problem is featured in the section "Using Systematic Casework" under Truth-Tellers and Liars , instead of checking for every possible case, there's a shorter way to do that is to eliminate options.
Consider the statements (2) and (4),
Ben says, "It wasn't Chris. It wasn't Emma." Dave says, "It was Chris. It was Ben."
Since each of the 5 statements is telling one truth and one lie, each of the above 2 statements provides us with two names one of which must be the accused. For example, take Ben's statement. If we assume the part "It wasn't Chris" to be true then "It wasn't Emma." is false and thus, Emma is the accused and when we assume the first part to be false then Chris is the one. Thus, we can infer these two conclusions:
From (2), either of Chris and Emma is the accused. From (4), either of Chris and Ben is the accused.
From (2) and (4), we conclude that Chris the accused.
It is said for every person, there is one truth with one lie. So knowing this knowledge we apply it to the question.
Alan says "it wasn't Emma. it was Ben" Lets assume "it wasn't Emma" is the true part of the statement ,that means "it was Ben" is a lie.
We next look Ben's statement.: "It wasn't Chris. It wasn't Emma." Since the assumption established is "it wasn't Emma" is true. To keep consistent with that assumption , the "it wasn't Emma" part of Ben's statement MUST BE TRUE. This implies that "It wasn't Chris" is a lie.
We next look at Chris's statement: "It was Emma. It wasn't Alan." Since the assumption established is "it wasn't Emma" is true. To keep consistent with that assumption , the "it was Emma" part of Chris's statement MUST BE FALSE. This implies that "It wasn't Alan" is a truth.
We next look at Dave's statement: "It was Chris. It was Ben." We know from the beginning "it was Ben" is a lie. from Alan's statement. To keep consistent with that result, the "It was Ben" part of Dave's statement MUST BE FALSE. This implies that "It was Chris" is a truth.
We lastly look at Emma: "It was Dave. It wasn't Alan." Since it has established "It wasn't Alan" is a truth, then "It was Dave" must be a lie.
In conclusion Chris ate the cake according to Dave.
You actually solved the problem in there paragraphs in fact only using two statemens, but your solution is unique because you 'double checked' the solution which I must say is an essential part of solving logic puzzles. By looking at so many solutions I am really surprised why only 53% were able to solve it.
I only looked at Ben and Dave, who got two positive statements and two negative statements respectively. The fact that they both lined up at Chris was just a huge hint telling me to break down the wall.
Start out assuming the first comment of the first person is true: It wasn't Emma. Therefore, given the aforementioned clue that one clause from each person is true and the other not true, his other clause "It was Ben" would not be true. If you look at Dave's stmt, "It was Ben" would also be false because it was decided in the previous stmt. Then, we take Dave's true stmt, "It was Chris" with a grain of salt because it assumes the final answer to the question. Ben then states "It wasn't Chris" which contradicts Dave's true stmt making this clause false and "It wasn't Emma" true--which is what we first assumed to be true. Everything else checks out.
From statements:
"It wasn't Chris. It wasn't Emma."
and,
"It was Chris. It was Ben."
For each of those statements you can see that one of the referred persons MUST have eaten the cake. CAREFUL, not could-have but must-have eaten the cake!
The only way for these statements to be both true, is their COMMON SOLUTION which is "Chris ate the cake".
From the 1st statement you can conclude that it wasn't Emma or Ben The second shows it's either Chris or Emma. So it's Chris.
If one statement from each is true and the other false, then for any of the people who gave an answer like "It wasn't X, it was Y" it follows that you automatically know that "It wasn't X" is true. To wit:
--if "it was Y" is true, then "it wasn't X" is false --which implies that "it was X", and therefore that it was BOTH X and Y. Can't happen.
Alan says "It wasn't Emma, it was Ben." Well, it wasn't Emma or Ben.
Ben says "It wasn't Chris, it wasn't Emma." We already know that "it wasn't Emma" is the true statement, therefore we negate the first half to find that it was Chris.
QED in two.
Ben and Dave give overlapping statements. Ben's statement means it HAD to be either Chris or Emma. Dave's statement means it HAD to be either Chris or Ben. Assuming it was Emma or Ben means either Ben (is we assume Emma did it) told the truth twice or Dave (if we assume Ben did it) lied twice.
Deduction via CONTRADICTION:
(1) Assume Ben from Dave's statement -> It wasn't Chris -> Deduce it was Emma from Ben's statement. CONTRADICTION -> It must be CHRIS
(2) Assume Emma from Ben's statement -> It wasn't Chris -> Deduce it was Ben from Dave's statement. CONTRADICTION -> It must be CHRIS
solved just by statement 2 and 4. Acc. to ben either chris or emma had it. similarly according to dave either chris or ben had it. thus CHRIS is the culprit .
So easy. Ben said it was not Chris and not Emma. So basically it is either Chris or Emma. Now Alan said it was not Emma, it is Ben. You know that second part is a lie. Therefore, it really isn't Emma, it is Chris.
Statements 1&2 . In S1 we learn it can't be Emma since either was both ate it or neither, so neither. S2 we know not Emma, is true therefore not Chris is false, or Chris ate it.
My solution is a bit different. I first looked for a double statement.
A person whose statement has 2 "was"es or 2 "wasn't"s, instead of 1 "was" and 1 "wasn't". Ben gave 2 "wasn't"s. Dave gave 2 "was"-es.
Since one sentence is true, and the other is false, and both statements will match, let's just start assuming.
According to Dave's statement, it was either Chris, or Ben. If Ben's first sentence, "It wasn't Chris." is true, then, the lie would be "It wasn't Emma.", and that would mean, "It was Emma." But, it's not Emma. Why? Because Dave said so!
drum roll
And there we have it, it's not Emma, it's Chris.
Consider statement one (alans statement). Either the first part is false and the second part is true or the first part is true and the second part is false. If the first part is false, the second part is true. If the first part is false we know that Emma ate the last slice, butif the first part is false the second part must be true, so Ben also ate the last slice. This isn't possible. So the first part of Alans statement has got to be true. Now move on to the second statement, we already established that Emma did not eat the last slice. So the second part of the second statement is true, and the first part must be false. So Chris ate the last slice.
First thing's first: If they say a two statements of which consists of it was someone and it wasn't someone else, it must mean both did not eat the cake. This is because if the "it was" is the lie, then both would be it wasn't. And, if the "it wasn't" is the lie, then both would have eaten the cake, which is impossible.
Second: If both statements are it was someone, then it has to be one of them, as one is the truth.
Third: If both statements are it wasn't someone, then it has to has to be one of them, as one is a lie.
Solution 1: Ben's statements show it is either Chris or Emma. Dave's statements show it is either Chris or Ben. Therefore it must be Chris
Solution 2: Ben's statements show it is either Chris or Emma. Alan's statement shows that Ben and Emma did not eat it. Therefore it must be Chris
Solution 3. Ben's statements show it is either Chris or Emma. Chris' statement shows it's neither Emma nor Alan. Therefore Chris ate it.
There are many other solutions, so feel free to add to what I missed!
A possible shorter way of getting to the answer. Assume the true statement from Alan was "It was Ben". If that were true, then both the statements Ben said would be true too contradicting the initial condition. So, for Alan, "It was Ben" is the lie, and "It wasn't Emma" is the truth. Knowing this, we can say that for Ben, "It wasn't Emma" is again the truth, hence "It wasn't Chris" must be the lie. So, Chris did it.