The Case Of The Missing Square

Relevant wiki: Length and Area - Composite Figures

Let $x$ represent the side length of square $ABCD$ . In the diagram, extend $CB$ to intersect $EF$ at $H$ . This creates rectangle $AEHB$ and rectangle $CHFG$ . Then $FG=EA+AD=(4+x)\text{ m}$ and $EH=DC=x\text{ m}$ .

$\large\begin{aligned} \text{Area of AEHB+Area of CHFG}&=\text{Remaining Area}\\ AE \times EH + CG \times FG&=92\\ 4x+8(4+x)&=92\\ 4x+32+8x&=92\\ 12x+32&=92\\ 12x&=60 \\ x&=5 \end{aligned}$

Since $x = 5\text{ m}$ , $DG = 8 + x = 13\text{ m}$ and $FG = 4 + x = 9\text{ m}$ . The original area of rectangle is: $\large DEFG = DG × F G = 13 × 9 = \boxed{\boxed{117\text{ m}^2}}$

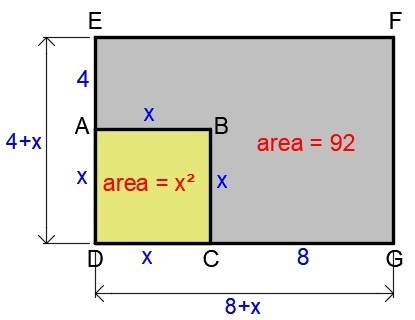From my diagram,

$(4+x)(8+x)=92+x^2$

$32+4x+8x+x^2=92+x^2$

$12x=60$

$x=5$

The dimensions of the triangle are $4+5=9$ and $8+5=13$ .

The area of the original rectangle is $9 \times 13 = \boxed{117~\text{m²}}$

Let AB = AD = a. Area ABCD = a x a. The area of the rest of the rectangle is (a x 4) = (a x 8) + 4 x 8 = 12a + 32. This is said to be 92. So 12a + 32 = 92. So 12a = 60. So a = 5. So the area of the whole rectangle is (5 + 4) x (5 + 8) = 9 x 13 = 117.