The Change Friction Makes In The Complexity Of A Problem.
 This problem has been inspired by a problem appearing in the
JEE ADV -2013
(Paragraph questions 13-14). The problem was quite easy because work done by friction had been given and conservation of energy could be easily applied. I tried to find out how the work done by friction is evaluated.This try led to the formation of the following problem:
This problem has been inspired by a problem appearing in the
JEE ADV -2013
(Paragraph questions 13-14). The problem was quite easy because work done by friction had been given and conservation of energy could be easily applied. I tried to find out how the work done by friction is evaluated.This try led to the formation of the following problem:
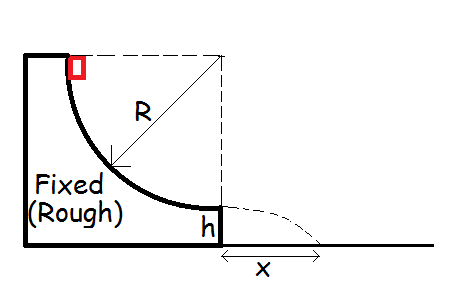
Consider a fixed wedge, whose part is a quarter circle of radius R as shown. A small block of mass m slides down the wedge and leaves horizontally from a height h as shown.The coefficient of friction between wedge and block is μ k . Compute the value of x in centimetres , where x is the distance from bottom of wedge of the point where the block falls given the values below:
Details
-
R = 2 0 0 c m
-
h = 1 0 5 c m
-
μ k = 0 . 5
-
m = 2 g
Round your answer to nearest integer
The answer is 89.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Discussions for this problem are now closed
good question
Excellent problem! (I wasn't able to solve it though) And a nice solution too!
I think it is tougher than many other level 5 problems
it looks a great solution, this solution is quite easier than my solution
simply apply work energy theorem and get velocity.
Work done by all forces =change in kinetic energy. W.D by gravity+work done by friction=1/2 mv^2 or conservation of M.E
taking reference lvl ash height above the ground
potential energy at top={energy dissipated by friction(W.D by friction)+kinetic energy at h height} this will get us velocity and we can find range of projectile after that.
it would be very difficult to calculate work done by friction.
Can i take Normal force as the average of N at the beginning(=0) and at the end point(=mg), i tried it and the answer was correct...
ya .its a good question
Please help me out! is the main difficulty in the integrating v^2dx ?
idea is simple but solving it by introducing a linear differential equation is the best part of the question
Great question
Brilliant problem !!! Unfortunately I couldn't integrate that.
@jatin yadav Nice solution, is this problem original?
All physics problems I have ever posted here are original.
@jatin yadav did you appear for IIT-JEE.
First of All, Beautiful question. Congratulation to the one who formed it. I thoroughly enjoyed solving it.
Now to the solution.
A schematic Diagram can be found here
As is apparent from the diagram the frictional force is μ ( M g S i n θ + M v 2 / R )
Using Newton's second Law,
M d t d v = M g C o s θ − μ ( M g S i n θ + M v 2 / R )
Dividing throughout by M ,
d t d v = g C o s θ − μ ( g S i n θ + v 2 / R )
And by rules of rotational dynamics,
v = R d t d θ
Eliminating d t from the equations we get,
v d θ d v = g R C o s θ − μ g R S i n θ − μ v 2
v d θ d v can be written as 2 1 d θ d v 2
which gives us the linear differential equation,
d θ d v 2 + 2 μ v 2 = 2 g R ( C o s θ − μ S i n θ )
Solving the equation for θ from 0 to π / 2 , we will get the required value of v
For its solution, the Integrating factor would be e 2 μ θ
Therefore,
v 2 e 2 μ θ ∣ ∣ ∣ ∣ 0 π / 2 = 2 g R ∫ 0 π / 2 e 2 μ θ ( C o s θ − μ S i n θ ) d θ
The Left hand side can be easily expanded as v 2 e μ π
To solve the Integral on the Right hand side, we designate the integral as I and apply Integration by parts twice
I = ∫ 0 π / 2 e 2 μ θ ( C o s θ − μ S i n θ ) d θ
Applying by parts,
I = 2 μ 1 ( e 2 μ θ ( C o s θ − μ S i n θ ) ∣ ∣ ∣ ∣ 0 π / 2 + ∫ 0 π / 2 e 2 μ θ ( S i n θ + μ C o s θ ) d θ )
This can be called as E q u a t i o n 1
The first term can be evaluated as e 2 μ θ ( C o s θ − μ S i n θ ) ∣ ∣ ∣ ∣ 0 π / 2 = − μ e μ π − 1
The integral can be evaluated as
∫ 0 π / 2 e 2 μ θ ( S i n θ + μ C o s θ ) d θ = 2 μ 1 ( e 2 μ θ ( S i n θ + μ C o s θ ) ∣ ∣ ∣ ∣ 0 π / 2 − ∫ 0 π / 2 e 2 μ θ ( C o s θ − μ S i n θ ) d θ )
The first term is e 2 μ θ ( S i n θ + μ C o s θ ) ∣ ∣ ∣ ∣ 0 π / 2 = e μ π − μ
and the second term is I itself.
Replacing in E q u a t i o n 1 ,
I = 2 μ 1 ( − μ e μ π − 1 + 2 μ 1 ( e μ π − μ − I ) )
On solving for I , we get
I = ( e π μ ( 2 μ 1 − μ ) − 2 3 ) / ( 2 μ + 2 μ 1 )
By putting the value of μ = 0 . 5 ,
I = 4 1 ( e π / 2 − 3 )
Putting its value in the original equation,
v 2 e μ π = g R 2 1 ( e π / 2 − 3 )
Therefore, the speed with which it is released from the ramp is
v = g R 2 1 − 3 e − π / 2
The range covered x = v g 2 h
Putting the value of v ,
x = h R ( 1 − 3 e − π / 2 )
Putting the value of h = 1 0 5 c m and R = 2 0 0 c m ,
We get x = 8 8 . 9 0 2 1 1 8 5 9 0 6
Approximating to the nearest integer,
x = 8 9
Wow!! 16 and 17 years teenagers are already known about ODE? It's surprising me. It looks like India does have a bright future in the hand of its young generation. Anyway, it took twice attempts for me to answer this problem. This was my first approach (I use the law of conservation energy instead of Newton 2nd law): m g ( h + R ) m g R − 2 1 m v f 2 g R − 2 1 v f 2 2 μ R 2 g R − v f 2 = m g h + 2 1 m v 2 + ∫ 0 2 π f R d θ = ∫ 0 2 π μ ( m g sin θ − R m v 2 ) R d θ = ∫ 0 2 π μ R ( g sin θ − R ( d t d θ ) 2 ) d θ = g − ∫ 0 2 π R ( d t d θ ) 2 d θ The last part is difficult for me to evaluate. What is wrong in my approach? Could you help me out? Thanks for any help you're able to provide.
Obviously, you need to know θ ( t ) to evaluate the last part.So, we take the other way to solve the problem..
In your energy conservation equation, rather analyse for a general angle θ rather than 2 π and then differentiate with respect to θ to get a LDE

First, we make the force diagram at the instant when then angle made by line joining center of circle, and block with horizontal is θ . The force diagram would be as shown. Let the speed of the block at this instant be v . Clearly, there would be two components of acceleration , centripetal and tangential.
We know that centripetal acceleration is given by R v 2 , hence we use Newton's law to get:
N − m g sin θ = R m v 2
⇒ N = m g sin θ + R m v 2
We know that f = μ k N , ⇒ f = μ k ( m g sin θ + R m v 2 ) .
Now, tangential acceleration = d t d v = v d t v d v = R d θ v d v = 2 R d θ d ( v 2 ) , hence, using Newton's law,
m g cos θ − μ k ( m g sin θ + R m v 2 ) = m 2 R d θ d ( v 2 )
Rearrange and divide by m to get:
d θ d ( v 2 ) + 2 μ k v 2 = 2 R g ( cos θ − μ k sin θ )
Clearly, this is a Linear Differential equation in v 2 and θ .
Integrating factor = e ∫ 2 μ k d θ = e 2 μ k θ
Hence the solution is given by:
v 2 e 2 μ k θ = 2 R g ∫ 0 θ e 2 μ k θ ( cos θ − μ k sin θ ) d θ
The right hand side can be easily evaluated , if you have already seen this post. Here, clearly, a = 2 μ k ; b = 1 .
Solving, we get:
v 2 = 4 μ k 2 + 1 2 R g ( 3 μ k ( cos θ − e − 2 μ k θ ) + ( 1 − 2 μ k 2 ) sin θ )
In our case, μ k = 0 . 5 , and we have to find the value of v at bottom (say v b ) , hence, θ = 2 π . Substituting these values,
v b = 2 R g ( 1 − 3 e − 2 π ) .
Now, using the formula for the range of a projectile given horizontal velocity from a given height, we get:
x = 2 R g ( 1 − 3 e − 2 π ) × g 2 h = R h ( 1 − 3 e − 2 π )
Substitute values to get : x ≈ 0 . 8 9 m = 8 9 c m