The 'Circle and Rectangle' Problem

Geometry Level 2

A circle and rectangle overlap such as the diagram given below.

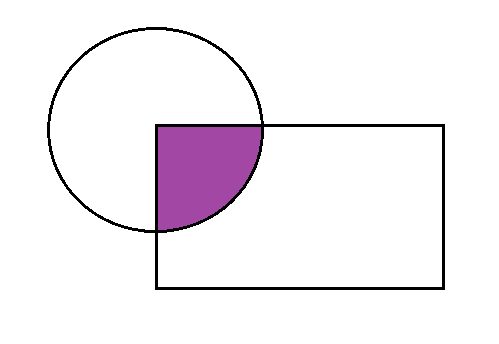
We are told that the circumference of the circle is 9.38 cm 9.38 \text{ cm} , and that the circle and rectangle have an equal geometrical area.

Assuming the overlapping region (region in purple) is a quarter of both the circle and rectangle, work out the area of the shaded region in cm 2 \text{cm}^2 .

Note: Give your answer to at least three significant figures.


The answer is 1.75.

Surayyah Aziz by Surayyah Aziz , 18, United Kingdom

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Surayyah Aziz
Aug 6, 2018

Solution: 1.75

Explanation:

  • 9.38 / π = diameter = 2.985746732

  • 1 2 \frac{1}{2} x diameter = radius ⇒ 2.985746732 / 2 = 1.492873366

  • Area of circle = π x r^2 = π x 1.492873366^2 = 0.1576087

  • 0.1576087 / 4 = 1.750394022 = Area of purple region

  • Answer is then given to 3 sig. figs = 1.75 cm^2

1 Helpful 0 Interesting 0 Brilliant 0 Confused

The rectangle is irrelevant. Why not just ask for the 1/4 of the area of the circle?

Milko Dyakov - 2 years, 10 months ago

Log in to reply

Hello, I apologise for the confusion. I just put the rectangle in to complicate the question a little, when actually reading the problem. As you have said, it has nothing to do with the answer, and can easily be ignored - which I hoped people would do if they had realised this. Thank you for sharing your concern, and yes the rectangle is irrelevant.

Surayyah Aziz - 2 years, 10 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...