The Circular Problem
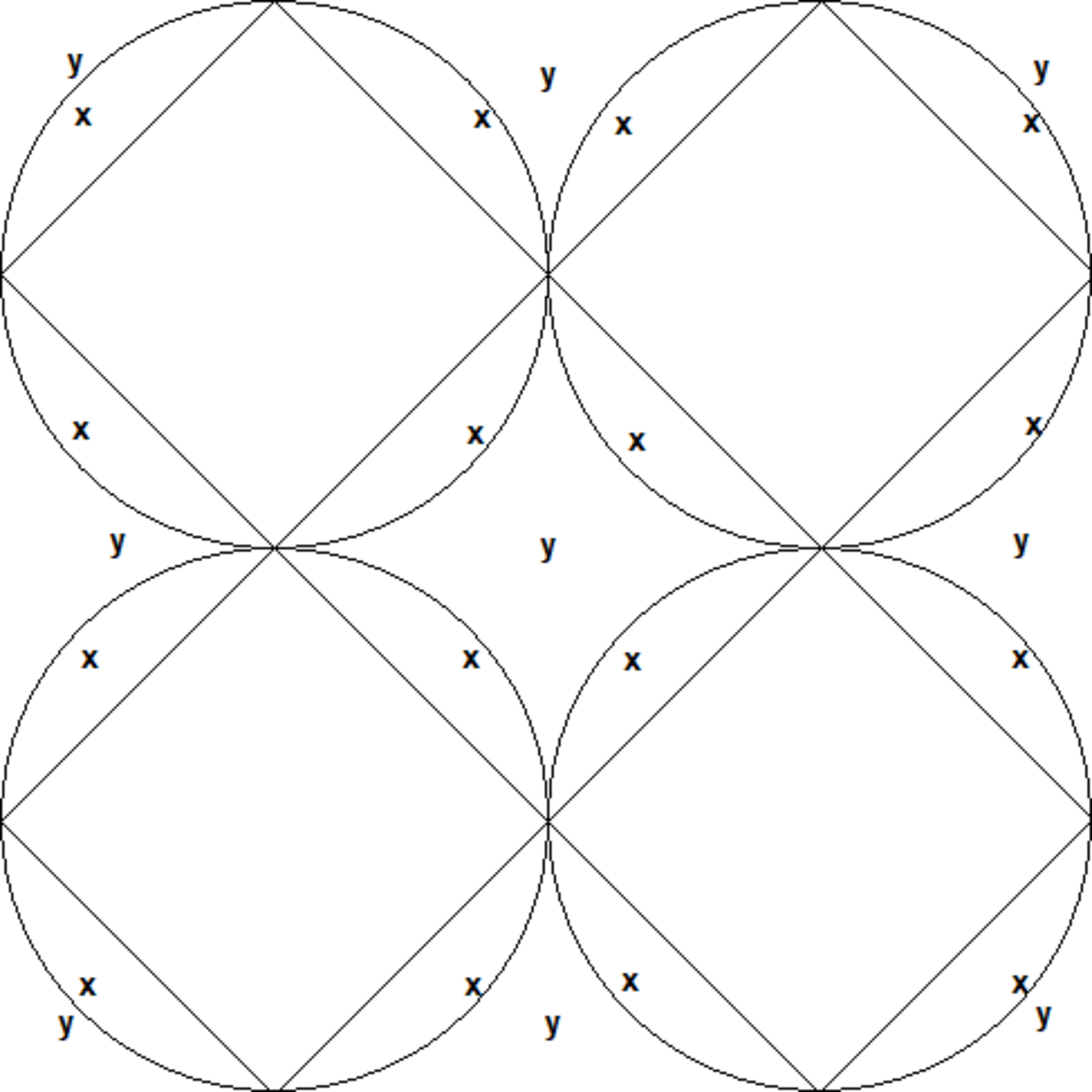
The above figure has an area of 49 square units. Regions outside the circles marked as 'y' and regions inside the circle but outside the diamonds marked as 'x'. Find the total area of the regions marked as 'x' and the total area of the regions marked as 'y'. Divide the total area of the regions marked as 'x' by the total area of the regions marked as 'y'. Multiply the result by 6 and then find the factorial of the result thus obtained.
The answer is 40320.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
It will be easier to draw the radii inside the circles to find the areas of the circles and the diamonds. If the area of the square = 49 square units, then the measure of one side of the square = 7 units.
Therefore, the measure of the radius = 4 7 units. Therefore, the area of the circle = 7 2 2 * 4 7 * 4 7 = 8 7 7 . Therefore, the total area of all the circles = 8 7 7 * 4 = 2 7 7 .
The total area of one quarter of a diamond = 2 1 * 4 7 * 4 7 = 3 2 4 9 . Therefore, the area of a diamond = 3 2 4 9 * 4 = 8 4 9 . Therefore, the total area of all the diamonds = 8 4 9 * 4 = 2 4 9 .
Therefore, the total area of the regions marked as 'x' = 2 7 7 - 2 4 9 = 2 2 8 .
Therefore, the total area of the regions marked as 'y' = 49 * 2 2 - 2 7 7 = 2 9 8 - 2 7 7 = 2 2 1 .
Therefore, 2 2 8 / 2 2 1 = 2 2 8 * 2 1 2 = 3 4
Therefore, 3 4 * 6 = 8
Therefore, 8! = 40320