The classic rope on table problem (with a twist)

Classical Mechanics Level 2

Difficulty: Good for learning how to formulate differential equations from systems. Medium level.

Most of us have tried this classical mechanics problem:

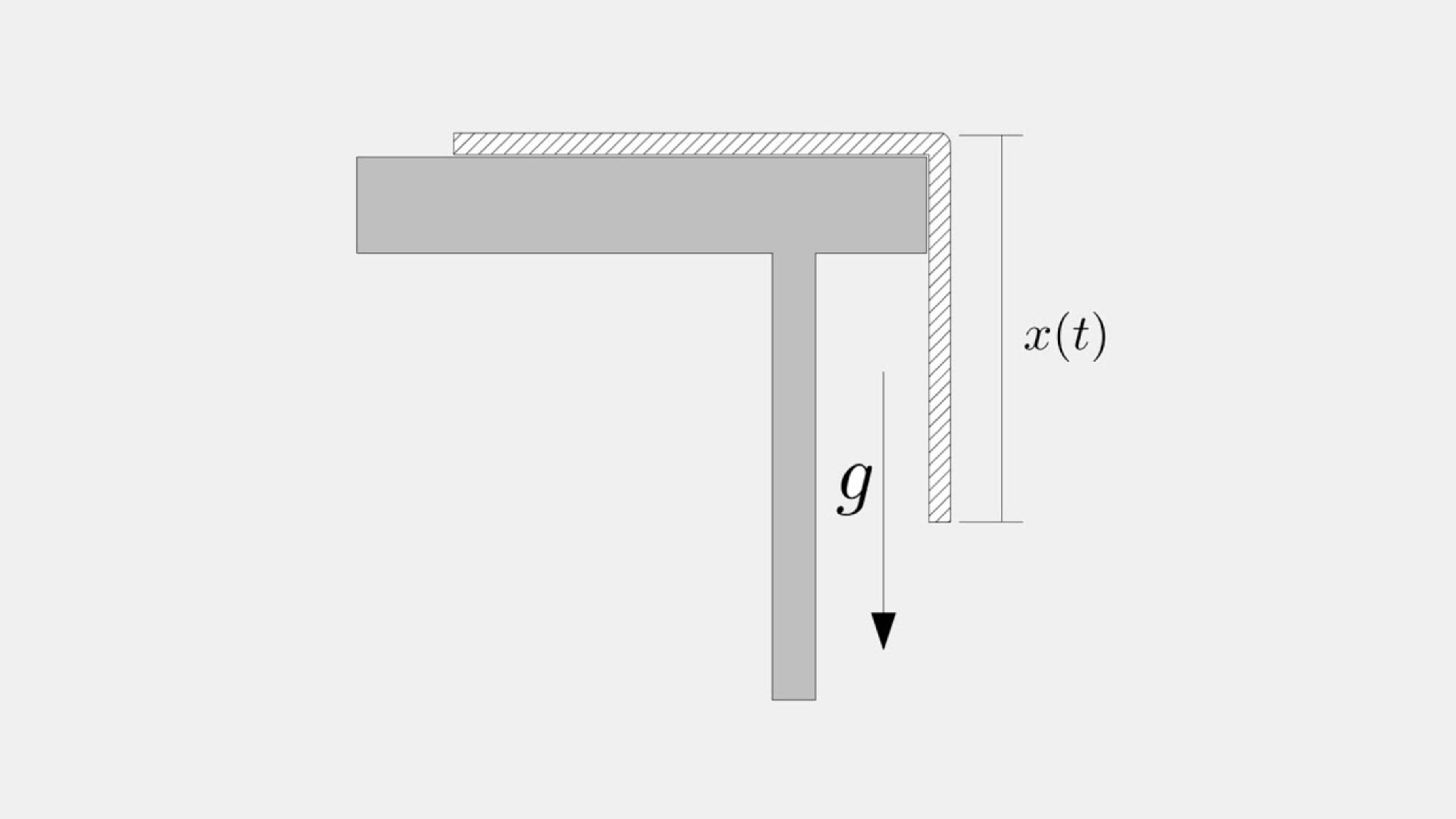
The rope sliding on table problem. The rope is of length $l$ meters and mass $m$ , and the hanging part is of length $x$ . However, this time, there is friction; find the time taken for the rope to fall off the table, ie. $x = l$ .

Enter your answer in seconds.

Relevant information:

$x_0 = 2$ meters (part of rope that is hanging)
$l = 10$ meters
$m = 10 kg$
Gravitational acceleration is $g = 10m/s^2$
Coefficient of friction (only on the table) is $\mu = 0.2$ ; friction force can be given by $\mu \bold{N}$
The string is of uniform density.

The answer is 3.5708.

2 solutions

Krishna Karthik
Aug 26, 2020

We can treat the rope as a pulley with two different masses; a mass on the table, and a hanging mass.

The hanging part's mass can be given mathematically by $\displaystyle \frac{x}{l} m$ , and the table part's mass is $\displaystyle \frac{l-x}{l} m$

Newton's 2nd law:

$\displaystyle \frac{x}{l}mg - \frac{l-x}{l}m \ddot{x} = \frac{x}{l}m \ddot{x}$

Solving the equation above yields:

$\displaystyle m \ddot{x} = \frac{x}{l}mg$

However, with friction, the equation of total force is:

$\displaystyle m \ddot{x} = \frac{x}{l}mg - \mu \frac{l-x}{l}mg$

Solving the equation numerically, with initial condition $x_0 = 2$ and $x_f = 10$ the time is $\boxed{3.5708}$ seconds.

@Krishna Karthik Did you have solved that 36 Newtonian mechanics problems?

Talulah Riley - 9 months, 1 week ago

Not yet. I'm busy with school work and only solved a few. Thanks mate :)

Krishna Karthik - 9 months, 1 week ago

@Bilu Bilu

Krishna Karthik - 9 months, 1 week ago

@Krishna Karthik who us bilu bilu?

Talulah Riley - 9 months, 1 week ago

An online friend. He's apparently on brilliant too. He's trying to learn advanced maths and physics.

Krishna Karthik - 9 months, 1 week ago

@Krishna Karthik Bro I want to change my name again?
But I am not able to change. Do you know how to change it again?

Talulah Riley - 8 months, 4 weeks ago

Talk to brilliant admin; they will help you with the name change. Send a letter to brilliant, and tell them the name you want to change to

Krishna Karthik - 8 months, 4 weeks ago

Karan Chatrath
Aug 27, 2020

The equation of motion is derived by @Krishna Karthik . I have not done anything fundamentally different. I have simply plugged in the parameters into the derived equation and numerically integrated it as shown:

clear all
clc

% Initial position and velocity of rope:
x(1)   = 2;
dx(1)  = 0;

% Time step:
dt     = 1e-6;

% Time and index initialisation:
t(1)   = 0;
k      = 1;


% Numerical integration till rope leaves the table:
while x(k) <= 10

    % Equation of motion:
    ddx = (6*x(k)/5) - 2;

    % Numerical integration for velocity:
    dx(k+1) = dx(k) + dt*ddx;

    % Numerical integration for position:
    x(k+1)  = x(k) + dt*dx(k+1);

    % Time and index increment:
    t(k+1)  = t(k) + dt;    
    k       = k + 1;
end

ANSWER = t(end)
% ANSWER = 3.5708 seconds

Nice numerical solution. Thanks mate :) (upvoted)

Krishna Karthik - 9 months, 2 weeks ago

Hi; I think you can read my response here. About my deleted problem, the equations of motion I got were:

(1) $m \ddot{x} = T \pm \mu N - F_s \cos{\theta}$

(2) $mg - T = m \ddot{x}$

Where $N = mg - F_s \sin(\theta)$

$T = mg - m \ddot{x}$ ; is that right?

I might repost the corrected version of this question soon.

@Krishna Karthik

Krishna Karthik - 8 months, 1 week ago

The classic rope on table problem (with a twist)

The answer is 3.5708.

2 solutions

0 pending reports