The Clever Cat

Computer Science Level 5

How many slices of the list in this file sum up to at least 32?

Details and Assumptions:

A slice is a contiguous selection of elements from an array. For example [4,5,6] is a slice of [1,2,3,4,5,6,7,8,9] but [3,4,5,7] is not.
An example of an acceptable slice in the above question would be [-23,5,20,21,18] . This slice can be found near the end of the array.
As an explicit example, in the case for "sum up to at least 2": gives [1,-2,3,-4,5] There are 6 such slices: [[1, -2, 3], [1, -2, 3, -4, 5], [-2, 3, -4, 5], [3], [3, -4, 5], [5]]

The answer is 71939.

9 solutions

Chew-Seong Cheong
Apr 10, 2015

I used the following Python coding. I think it is simple.

s = [-22,-26,16,8,7,...] 

    n = 0
    for i in range(len(s)):
        x = 0
        for j in range(i,len(s)):
            x += s[j]
            if x >= 32:
                n += 1
    print n

It is.

How can we improve on the number of operations performed?

Agnishom Chattopadhyay - 5 years, 8 months ago

I have not thought about it.

Chew-Seong Cheong - 5 years, 8 months ago

Brian Rodriguez
Jul 14, 2015

# array = [-22, -26, 16...]
def solution(): # O(n^2)
    partial_sums = list(itertools.accumulate(array))
    slices = 0
    threshold = 32
    for lo in range(len(array)):
        for hi in range(lo, len(partial_sums)):
            if partial_sums[hi] >= threshold:
                slices += 1
        threshold += array[lo]
    return slices

print(solution())

Doesn't this code evaluate every possible slice of the list?

Josh Silverman Staff - 5 years, 10 months ago

nah, just the partial sums.
using: sum(array[lo:hi]) == sum(array[:hi]) - sum(array[:lo]) , it goes through each partial sum of the array and searches for another that would give it a difference greater than or equal to 32.
since there are n elements to consider and n partial sums, the algorithm runs in $O({ n }^{ 2 })$ time without ever recalculating a slice's sum.

side note: although I changed the code, the first one had the same complexity; it walked through a dict w/ partial sums as keys, and a list of indices where they appear as values. the new one just walks through the partial sums linearly (I realized I was over-complicating things w/ the dict thanks to Chew-Seong Cheong's answer :p)

Brian Rodriguez - 5 years, 10 months ago

David Holcer
Apr 8, 2015

#array=[set of number]
def totall(array,num):
    total=0
    for n in xrange(1,len(array)+1):
        for i in xrange(len(array)):
            cur=array[i:i+n]
            if len(cur)==n:
                summ=0
                for i in cur:
                    summ+=i
                if ((summ>=num) and (len(cur)==n)): total+=1
    return total
print totall(array,32)

Yay level 5 lol, its jest sub-array checking. I posted basic function and tweaked to problem. Just replace array with set of numbers, and 32 with target.

Give it time to settle. Especially since the answer was wrong (updated twice) the ratings could be off.

Calvin Lin Staff - 6 years, 2 months ago

Laurent Shorts
Feb 17, 2017

Python code

arr = [-22,-26,16, … 21,18,32]

def simple():
    n = 0
    for a in range(len(arr)):
        for b in range(a, len(arr)):
            if sum(arr[a:b+1]) >= 32:
                n += 1
    print n

def faster():
    sums = [0]
    for i in range(len(arr)):
        sums += [sums[-1] + arr[i]]   # or use itertools.accumulate
    n = 0
    for a in range(len(sums) - 1):
        for b in range(a+1, len(sums)):
            if sums[b] - sums[a] >= 32:
                n += 1
    print n

Masbahul Islam
Aug 22, 2016

a=open("list-GfO0iB928U.txt","r")

b=a.readline().split(",")

c=[]

for i in b:

c.append(int(i))

count=0

for x in range(1,len(c)+1):

 for y in range(len(c)-x+1):

     m=sum(c[y:y+x])

     if m>=32:

         count+=1

print count

Roel Baars
Jul 2, 2015

Nice and compact, but also a bit slow. Mathematica

1 2	`list = {-22, -26, 16, ...}; Sum[Count[Partition[list, n, 1], x_ /; Total[x] >= 32], {n, 1, Length[list]}]`

Arulx Z
May 14, 2015

final static int n[] = {-22,-26,16...}; //the array
public static void main(String args[]) {
    ArrayList<int[]> r = new ArrayList<int[]>();
    System.out.println(n.length);
    for(int i = 0; i <= n.length; i++)
        for(int j = 1; j + i <= n.length; j++)
            r.add(jump(j, j + i));  
    int tots = 0;       
    for(int[] a : r){
        int sum = 0;
        for(int b : a)
            sum += b;
        if(sum >= 32)
            tots++;
        sum = 0;
    }
    System.out.println(tots);
}

private static int[] jump(int start, int end){
    int array[] = new int[end - start + 1];
    for(int i = start - 1, j = 0; i < end; i++, j++)
        array[j] = (n[i]);
    return array;
}

Bill Bell
Apr 17, 2015

This is a problem for which a so-called sliding window iterator is a good part of a solution. As someone first said, 'Good programmers are lazy.' Accordingly, I've copied code from http://stackoverflow.com/questions/6822725/rolling-or-sliding-window-iterator-in-python.

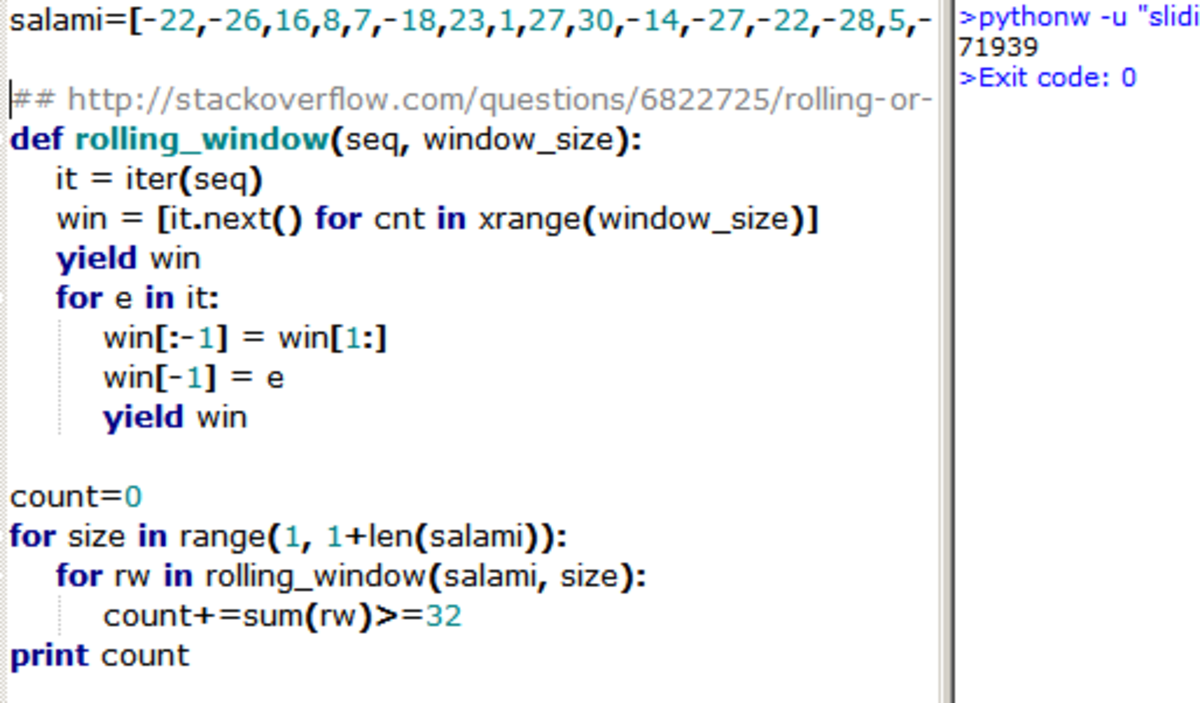
I don't know if this is by any means the fastest iterator for this job.

Alex Li
Apr 13, 2015

public class x 
{
    public static int sum(int[] z, int x, int y)
    {
        int total = 0;
        for(int i = x; i < y; i++)
        {
            total += z[i];
        }
        return total;
    }
    public static void main(String[] args)
    {
        int[] a = {-22,-26,...};
        int total = 0;
        for(int i = 0; i < a.length; i++)
        {
            for(int j = i + 1; j <= a.length; j++)
            {
                if(sum(a, i, j) >= 32)
                {
                    total++;
                }
            }
        }
        System.out.println(total);
    }
}

The Clever Cat

The answer is 71939.

9 solutions

0 pending reports