A genius solution!
Given that a , b and c are real numbers such that a b c = 1 , find the value of ( a b + a + 1 a + b c + b + 1 b + c a + c + 1 c ) 2 .
The answer is 1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
16 solutions
How did the ab/abc+ab+a and the abc/abca+abc+ab be . Ab/1+ab+ a ? Please explain tnx
creative way to substitute data
Actually this solution needs to prove that a,b and c can't be equal to zero
I has a mistake..!
I have seen this on Chinese maths books... Amazing
i did the same
it is given that abc=1 that means a=1, b=1, c=1 and the solution is too much easy then. :P
Log in to reply
It Is Given That abc=1 That Doesn't Necessarily Mean a=b=c=1(Ex. a=3, b=1, c=1/3) , However You Can Assume a=b=c=1 For This Problem.
what if a=1/2,b=2 and c=1?
Another simplification is obtained by putting a = x/y, b = y/z and c = z/x, which gives same denominator, so that adding becomes easy..
Sir write all your mathematical text incased in ( and \ ) such that there is no gap between the \ and ) , while writing a problem or a solution there is written with small letters in a corner - Formatting guide , so take help from it , or right click a problem and open it in a new window and click your avatar , there comes toogle latex you can copy latex from it(or you may refer from it) , start it now it takes time to collaborate but then you will get used to it - I am saying this because sometimes yours solution are very good , but if someone have written in latex , many don't see the rest , for example here only see Luke's tan method , he posted 4 hours before Victor Loh , but he gets only 2 upvotes , you too can see it , just observe , the writing by Victor loh seems very beautiful , most get impressed at very first sight , and don't see others approach which can be better than theirs
Thank you and sorry if I have said something wrong @Rajen Kapur
Is it a valid approach to consider b=1, thus a=1/c, then study the limit as either a or c gets bigger?
Great this is really nice
Since they said that all the numbers are real values, as abc = 1, I can say that a = 1, b = 1, c = 1. As you sub in to the respective alphabeths, you will get, ((1/3) + (1/3) + (1/3))^2 = (1)^2 = 1
a=1 b=1/2 c=2 abc=1 there are infinite possible sets of a ,b ,c with that answer assuming like that is wrong real numbers are all numbers even irrational numbers so a=1 b=root2 c=1/root2 is also accepted in {abc=1 abc belong to real no.} your method would be correct if it was natural numbers or integers otherwise it is wrong
Log in to reply
His method isn't wrong just because there are other possibilities. With only one equation for 3 unknowns, there are 2 free variables. No assumption is 'wrong' as long as abc=1. Since the question imposed the expression had a single answer without sufficiently defining a, b, or c, any set that satisfies abc=1 should and does give the answer.
I noticed that, for example, a b + a + 1 a = a b + a + a b c a = a ( b + 1 + b c ) a = b c + b + 1 1 so there is a cyclic relation between the terms, which leads to making equal the numerator and the denominator.
Multiplying the top and bottom of b c + b + 1 b by a and the top and bottom of c a + c + 1 c ) 2 by ab, we get ( a b + a + 1 a + b c + b + 1 b + c a + c + 1 c ) 2 =( a b + a + 1 a + a b c + a b + a a b + a 2 b c + a b c + a b a b c ) 2 =( a b + a + 1 a b + a + 1 ) 2 =( 1 ) 2 =1
There's no need to assign any values for A , B & C , but we can solve for them as follows : a b + a + 1 a = a b + a + a b c a = b c + b + 1 1 and b c + b + 1 b = b c + b + a b c b = a c + c + 1 1 and c a + c + 1 c = c a + c + a b c c = a b + a + 1 1 and one finds from these equations that : a b + a + 1 a ≡ ( c a + c + 1 c ) a and c a + c + 1 c ≡ ( b c + b + 1 b ) c and b c + b + 1 b ≡ ( a b + a + 1 a ) b from these equations we can formulate the question in a different form : a c + c + 1 a c + a b + a + 1 a b + b c + b + 1 b c and we can try to unify all of these by multiplying each fraction by the term its missing : a b c + b c + b a b c + a b c + a c + c a b c + a b c + a b + a a b c and since abc =1 , the last equation becomes : 1 + b c + b 1 + 1 + a c + c 1 + 1 + a b + a 1 and from that we can equate the coefficients for A , B & C from the question itself to find that A = 1 , B = 1 , C = 1
and from the last equation we can substitute the values we obtained to get : 3 1 + 3 1 + 3 1 = 1 and by squaring it , we get one !
If the answer is the same regardless of the actual values of a, b, and c, make them all equal to 1, which satisfies abc = 1. Then the answer becomes very obvious.
A naive approach: Since a , b , and c can be any real numbers for which we know that ( a b + a + 1 a + b c + b + 1 b + c a + c + 1 c ) 2 = c o n s t a n t ; therefore, we can simply take any random values for a , b , and c , say a = b = c = 1 , such that a b c = 1 and substitute in it as follows; ( a b + a + 1 a + b c + b + 1 b + c a + c + 1 c ) 2 = ( 1 + 1 + 1 1 + 1 + 1 + 1 1 + 1 + 1 + 1 1 ) 2 = ( 3 1 + 3 1 + 3 1 ) 2 = 1
 I don't know if that's clear but here you go
I don't know if that's clear but here you go
( a b + a + 1 a + b c + b + 1 b + c a + c + 1 c ) 2 .
⇒ ( a b + a + a b c a + b c + b + a b c b + c a + c + a b c c ) 2
= ( b + 1 + b c 1 + c + 1 + a c 1 + a + 1 + a b 1 ) 2
= ( b + 1 + b c 1 + c + 1 + a c 1 + a + 1 + a b 1 ) 2
= ( a b + a + 1 1 + b c + b + 1 1 + c a + c + 1 1 ) 2 ⇔ ( a b + a + 1 a + b c + b + 1 b + c a + c + 1 c ) 2
The expression is cyclic. By comparing terms we get that
( a , b , c ) = ( 1 , 1 , 1 )
Hence the expression is equal to:
( 3 1 + 3 1 + 3 1 ) 2 = 1 .
For starter,
a ∗ b ∗ c = 1 therefore a = 1 & b = & c = 1
Therefore,
( 3 1 + 3 1 + 3 1 )² = 1
If abc = 1, then you know that a = 1, b = 1, and c = 1. Therefore, substitute 1 in the place of each variable. Once you do that, then you should have ( 3 1 + 3 1 + 3 1 )^2. Add the fractions, and you get 3 3 or 1. 1^2 = 1.
Maybe I'm missing the point here, but just by looking at this one logic seems much quicker. If a,b,c are real numbers and abc=1 then we know all the numerators are 1. A quick glance at the denominators and they are all the same as well:
(
1
∗
1
)
+
(
1
)
+
1
=
3
So now we've got...
(
3
1
+
3
1
+
3
1
)
2
=
(
1
)
2
=
1
( a b + a + 1 a + b c + b + 1 b + a c + c + 1 c ) 2 = ( a b + a + 1 a + b c + b + 1 b × a a + a c + c + 1 c × c 1 c 1 ) 2
= ( a b + a + 1 a + a b + a + 1 a b + a c + c + 1 1 ) 2
= ( a b + a + 1 a b + a + 1 ) 2
= 1

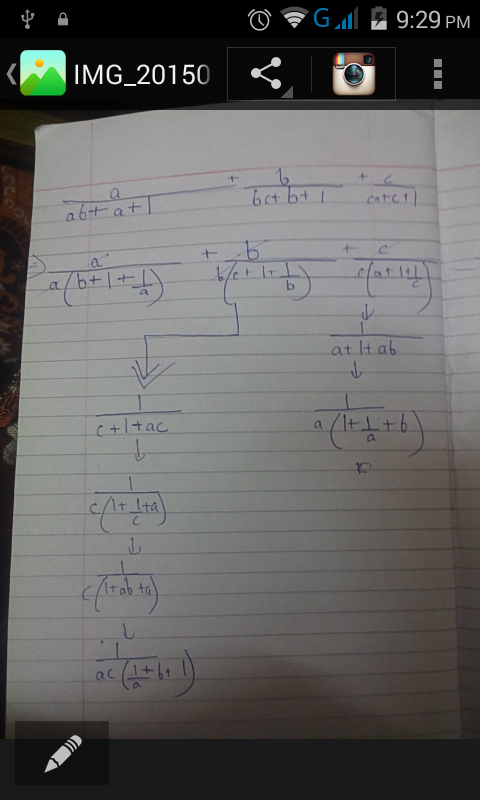

( a b + a + 1 a + b c + b + 1 b + c a + c + 1 c ) 2
= [ a b + a + 1 a + ( b c + b + 1 ) ( a ) b ( a ) + ( c a + c + 1 ) ( a b ) c ( a b ) ] 2
= ( a b + a + 1 a + a b c + a b + a a b + a b c a + a b c + a b a b c ) 2
= ( a b + a + 1 a + 1 + a b + a a b + a + 1 + a b 1 ) 2
= ( a b + a + 1 a b + a + 1 ) 2
= 1 2 = 1