The cosine of the angle between r and s is equal to
Let γ be the circle of equation x 2 + y 2 = 4 . If r , s are two lines intersecting at point P = ( 1 , 3 ) and are tangent to γ , then find the cosine of the angle between r and s .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
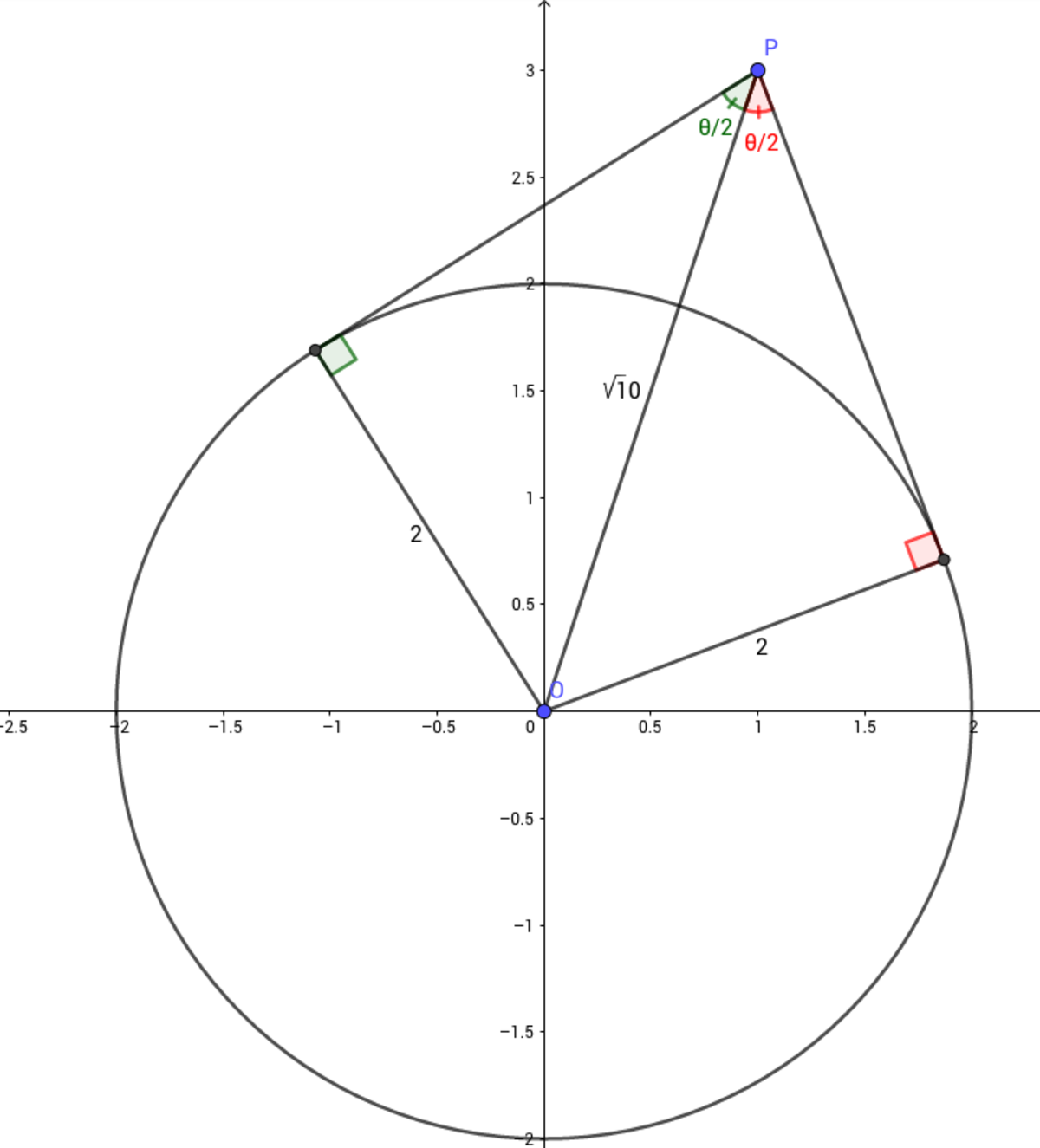 from observing the right triangles, we have
sin
(
2
θ
)
=
1
0
2
→
cos
(
θ
)
=
1
−
2
sin
2
(
2
θ
)
=
5
1
from observing the right triangles, we have
sin
(
2
θ
)
=
1
0
2
→
cos
(
θ
)
=
1
−
2
sin
2
(
2
θ
)
=
5
1
Given that the circle has equation x^2 + y^2 = 4, a calculation shows that the slope of the tangent lines at the points of tangency are dy/dx = -x/y. So, if the points of tangency are (x1, y1) and (x2, y2), we find the equations of r and s are respectively y - y1 = -x1 (x-x1)/y1 and y-y2 = -x2 (y - y2)/y2. Given that point (1,3) is on line r, some algebra then shows that (3-y1) y1 = -x1 (1-x1), or 3 y1 + x1 = x1^2 + y1^2 = 4 (with the last equality following from the fact that (x1, y1) is on the circle). Thus, x1 = 4 - 3 y1. Substituting this last equation into the equation of the circle and simplifying shows that the points of tangency are A((2-3 sqrt(6)/5, (6+sqrt(6)/5)), and B((2+3 sqrt(6))/5, (6-sqrt(6))/5). We can now find the vectors PA = A-P and PB = B - P. A calculation then shows that the dot product of PA and PB divided by the product of the norms of PA and PB, which is known to be the cosine of the angle between PA and PB, is 1/5.