The Cube Life of Hexagon Flowers
Regular hexagons can be put together in a flower-like way:
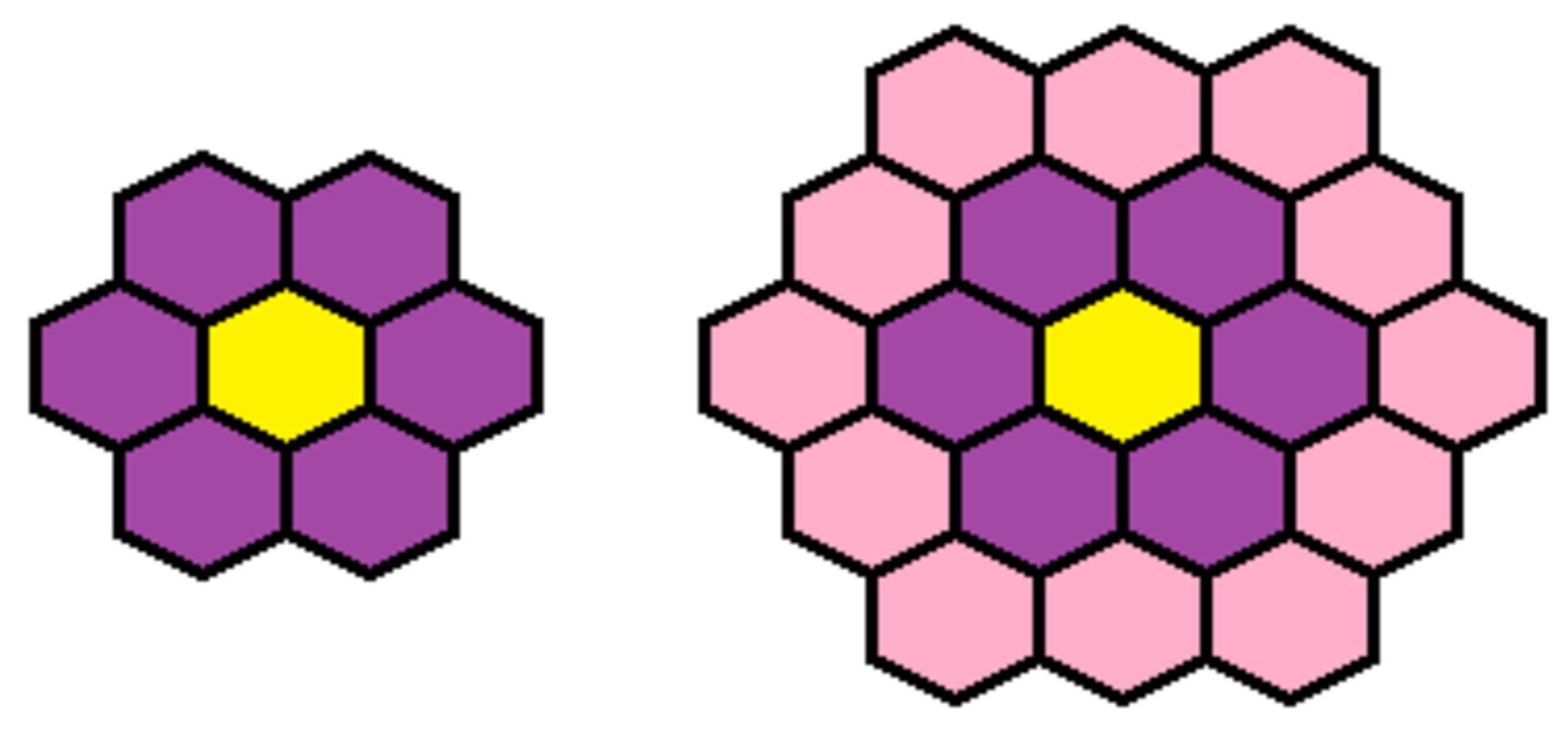
From the picture above you can see that hexagons are necessary to build the hexagon-flower on the left, and hexagons are necessary to build the hexagon-flower on the right.
Neither nor are perfect cubes. As we add more hexagons to make larger hexagon-flowers, will we ever be able to make a hexagon-flower whose total amount of hexagons is a perfect cube ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.

The number of regular hexagons used follows the sequence a n = 3 n ( n + 1 ) + 1 = ( n + 1 ) 3 − n 3 . See the solution in the Inspiration link for the proof.
Suppose a n can be expressed as a (positive) perfect cube, then this would contradict Fermat's last theorem , which is absurd!